Sparse Linear Regression

A demonstration of sparse linear regression using SparseReg toolbox. Sparsity is in the general sense: variable selection, total variation regularization, polynomial trend filtering, and others. Various penalties are implemented: elestic net (enet), power family (bridge regression), log penalty, SCAD, and MCP.

Contents

Sparse linear regression (n>p)

Simulate a sample data set (n=500, p=100)

clear;
s = RandStream('mt19937ar','Seed',1);
RandStream.setGlobalStream(s);
n = 500;
p = 100;
X = randn(n,p);             % generate a random design matrix
X = bsxfun(@rdivide, X, sqrt(sum(X.^2,1))); % normalize predictors
X = [ones(size(X,1),1) X];  % add intercept
b = zeros(p+1,1);           % true signal:
b(2:6) = 3;                 % first 5 predictors are 3
b(7:11) = -3;               % next 5 predictors are -3
y = X*b+randn(n,1);         % response vector

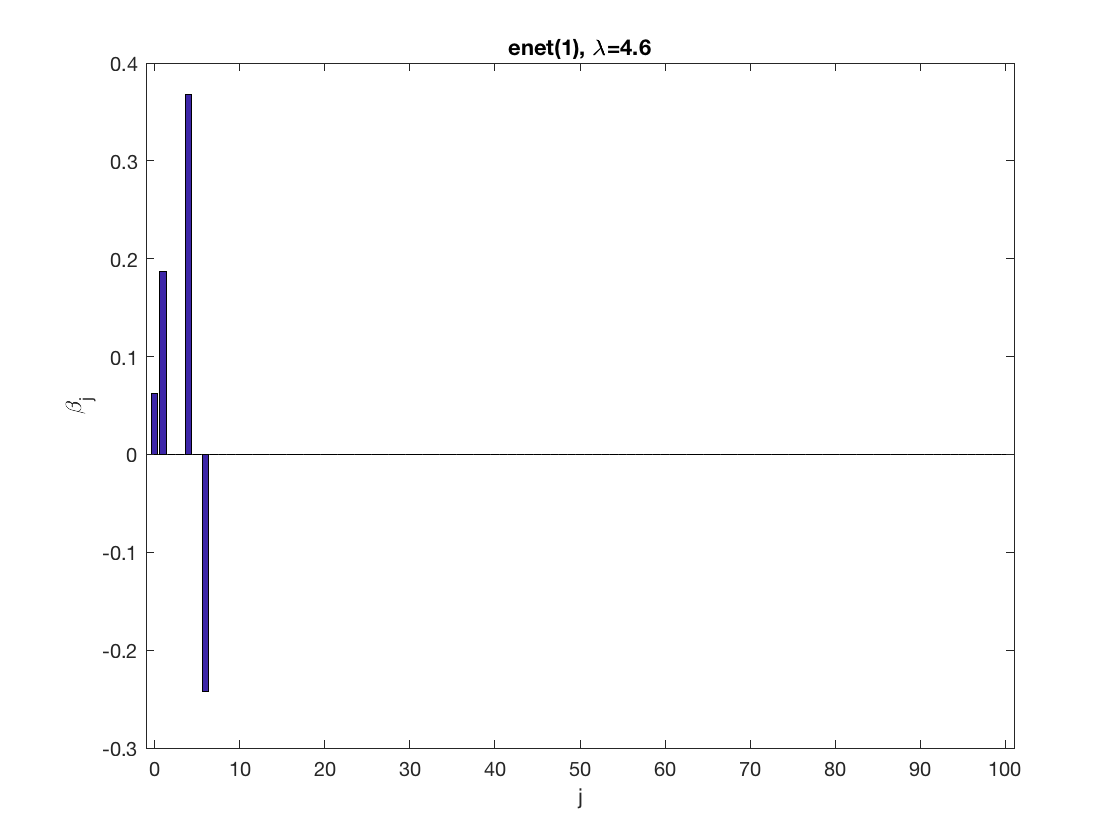
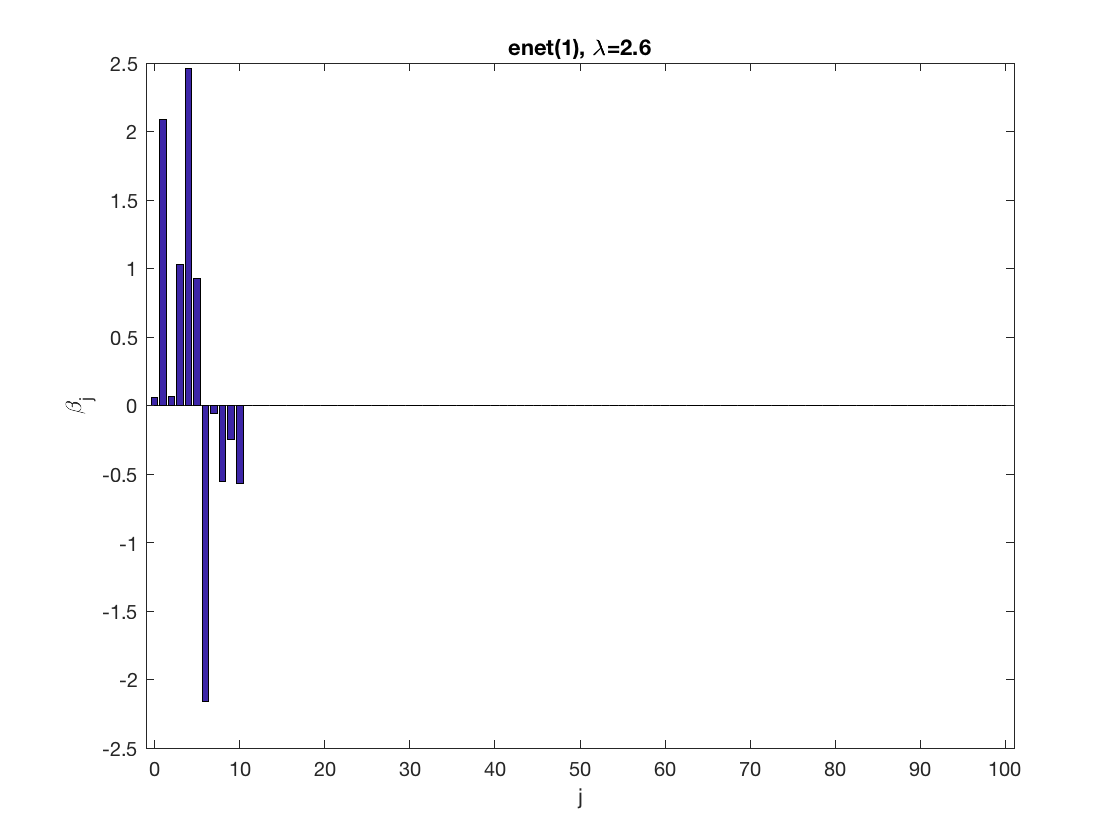
Sparse regression at a fixed tuning parameter value

penalty = 'enet';           % set penalty function to lasso
penparam = 1;
penidx = ...                % leave intercept unpenalized
    [false; true(size(X,2)-1,1)];
lambdastart = ...           % find the maximum tuning parameter to start
    max(lsq_maxlambda(sum(X(:,penidx).^2),-y'*X(:,penidx),penalty,penparam));
display(lambdastart);

lambda = 0.9*lambdastart;   % tuning parameter value
betahat = ...               % lasso regression
    lsq_sparsereg(X,y,lambda,'penalty',penalty,'penparam',penparam,'penidx',penidx);
figure;                     % plot penalized estimate
bar(0:length(betahat)-1,betahat);
xlabel('j');
ylabel('\beta_j');
xlim([-1,length(betahat)]);
title([penalty '(' num2str(penparam) '), \lambda=' num2str(lambda,2)]);

lambda = 0.5*lambdastart;   % try a smaller tuning parameter value
betahat = ...               % sparse regression
    lsq_sparsereg(X,y,lambda,'penalty',penalty,'penparam',penparam,'penidx',penidx);
figure;                     % plot penalized estimate
bar(0:length(betahat)-1,betahat);
xlabel('j');
ylabel('\beta_j');
xlim([-1,length(betahat)]);
title([penalty '(' num2str(penparam) '), \lambda=' num2str(lambda,2)]);

lambdastart =

    5.1621

Solution path for lasso

penalty = 'enet';           % set penalty function
penparam = 1;
penidx = [false; true(size(X,2)-1,1)];  % leave intercept unpenalized
tic;
[rho_path,beta_path] = ...  % compute solution path
    lsq_sparsepath(X,y,'penalty',penalty,'penparam',penparam,'penidx',penidx);
timing = toc;

figure;
plot(rho_path,beta_path);
xlabel('\rho');
ylabel('\beta(\rho)');
xlim([min(rho_path),max(rho_path)]);
title([penalty '(' num2str(penparam) '), ' num2str(timing,2) ' sec']);

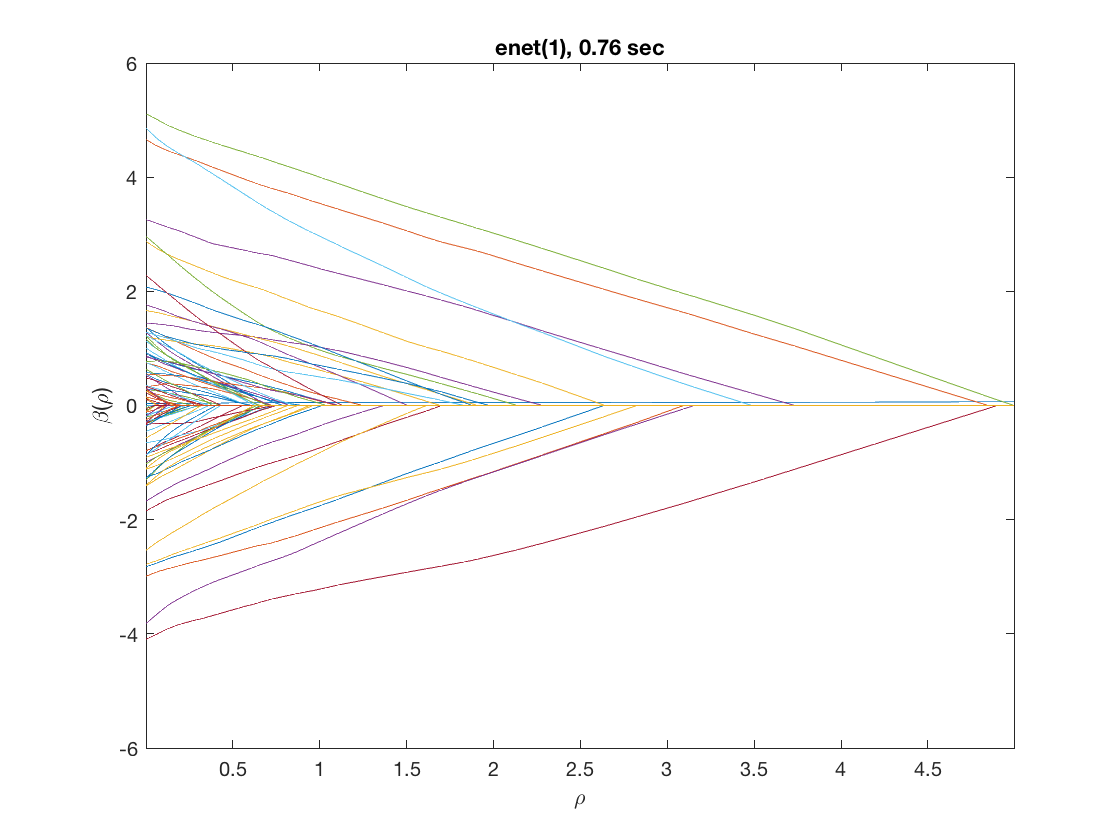
Solution path for power (0.5)

penalty = 'power';          % set penalty function to power
penparam = 0.5;
tic;
[rho_path,beta_path] = ...
    lsq_sparsepath(X,y,'penalty',penalty,'penparam',penparam,'penidx',penidx);
timing = toc;

figure;
plot(rho_path,beta_path);
xlabel('\rho');
ylabel('\beta(\rho)');
xlim([min(rho_path),max(rho_path)]);
title([penalty '(' num2str(penparam) '), ' num2str(timing,2) ' sec']);

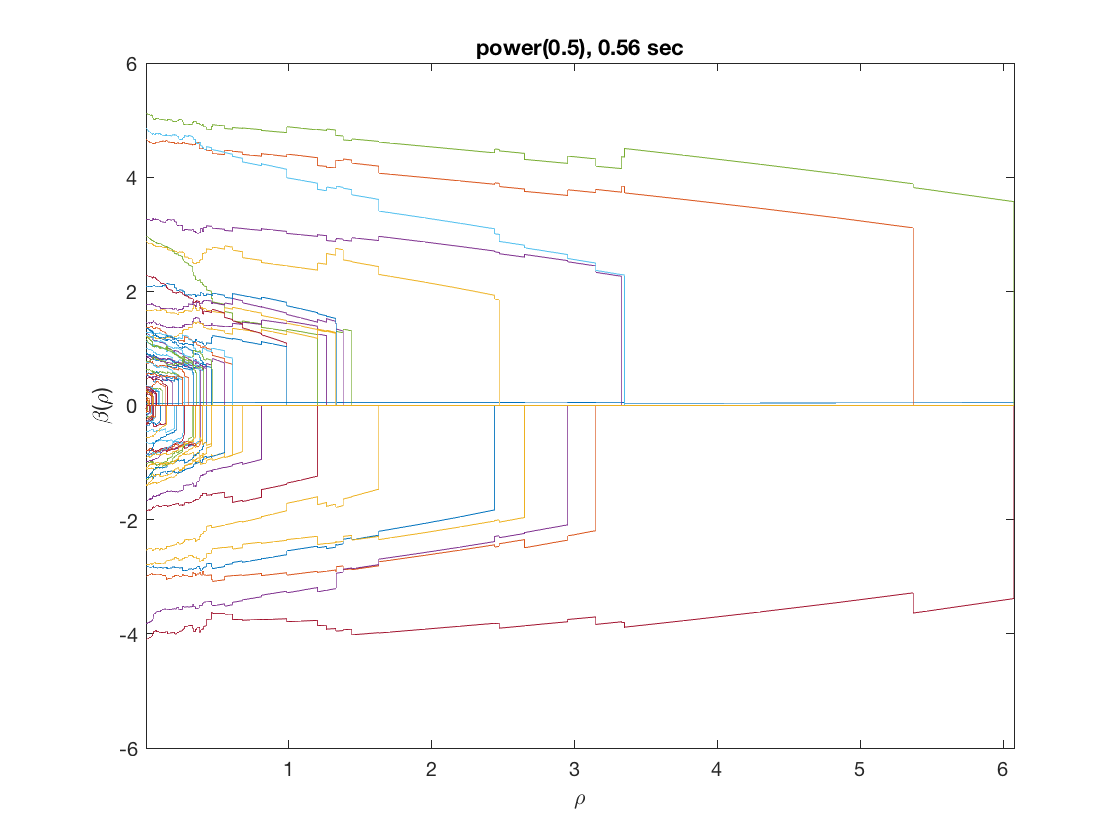
Compare solution paths from different penalties

penalty = {'enet' 'enet' 'enet' 'power' 'power' 'log' 'log' 'log' 'scad'};
penparam = [1 1.5 2 0.5 1 0 1 5 3.7];
penidx = [false; true(size(X,2)-1,1)];  % leave intercept unpenalized

figure
for i=1:length(penalty)
    tic;
    [rho_path,beta_path] = lsq_sparsepath(X,y,...
        'penalty',penalty{i},'penparam',penparam(i),'penidx',penidx);
    timing = toc;
    subplot(3,3,i);
    plot(rho_path,beta_path);
    if (i==8)
        xlabel('\rho');
    end
    if (i==4)
        ylabel('\beta(\rho)');
    end
    xlim([min(rho_path),max(rho_path)]);
    title([penalty{i} '(' num2str(penparam(i)) '), ' num2str(timing,1) 's']);
end

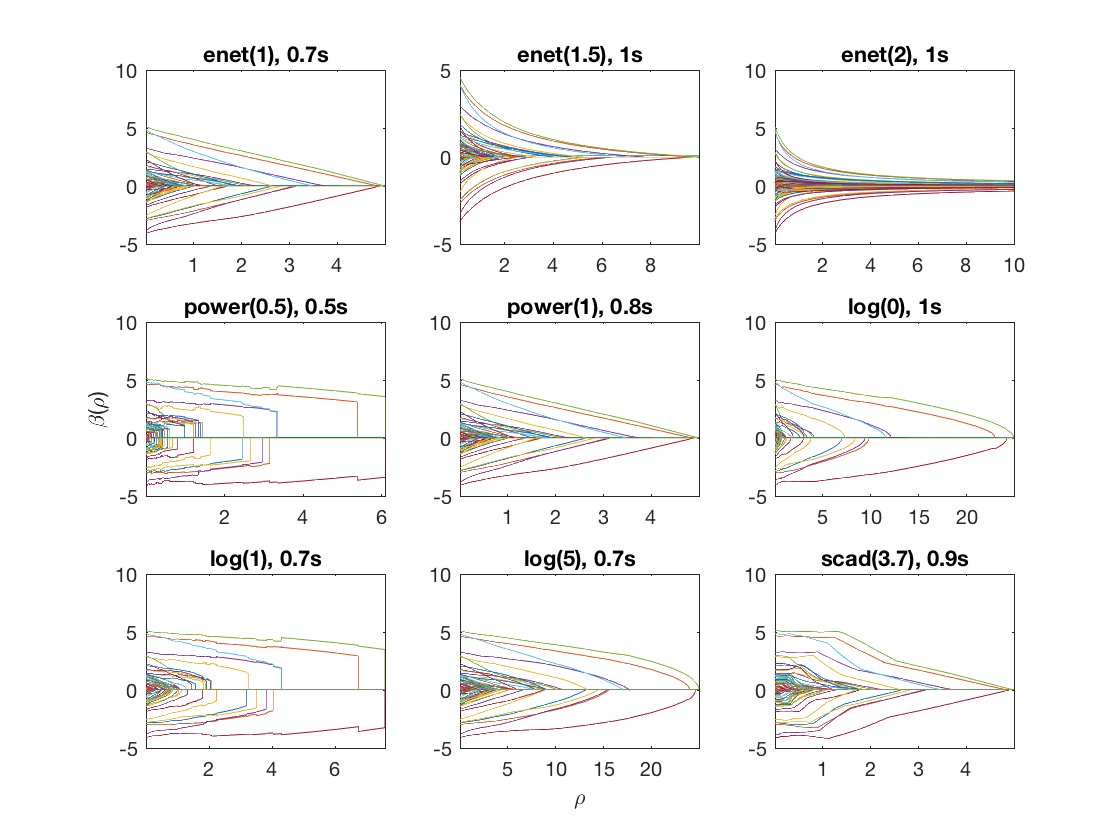
Fused linear regression

Fused lasso (fusing the first 10 predictors)

D = zeros(9,size(X,2));     % regularization matrix for fusing first 10 preds
D(10:10:90) = 1;
D(19:10:99) = -1;
display(D(1:9,1:11));
penalty = 'enet';           % set penalty function to lasso
penparam = 1;
tic;
[rho_path, beta_path] = lsq_regpath(X,y,D,'penalty',penalty,'penparam',penparam);
timing = toc;

figure;
plot(rho_path,beta_path(2:11,:));
xlabel('\rho');
ylabel('\beta(\rho)');
xlim([min(rho_path),max(rho_path)]);
title([penalty '(' num2str(penparam) '), ' num2str(timing,2) ' sec']);

     0     1    -1     0     0     0     0     0     0     0     0
     0     0     1    -1     0     0     0     0     0     0     0
     0     0     0     1    -1     0     0     0     0     0     0
     0     0     0     0     1    -1     0     0     0     0     0
     0     0     0     0     0     1    -1     0     0     0     0
     0     0     0     0     0     0     1    -1     0     0     0
     0     0     0     0     0     0     0     1    -1     0     0
     0     0     0     0     0     0     0     0     1    -1     0
     0     0     0     0     0     0     0     0     0     1    -1

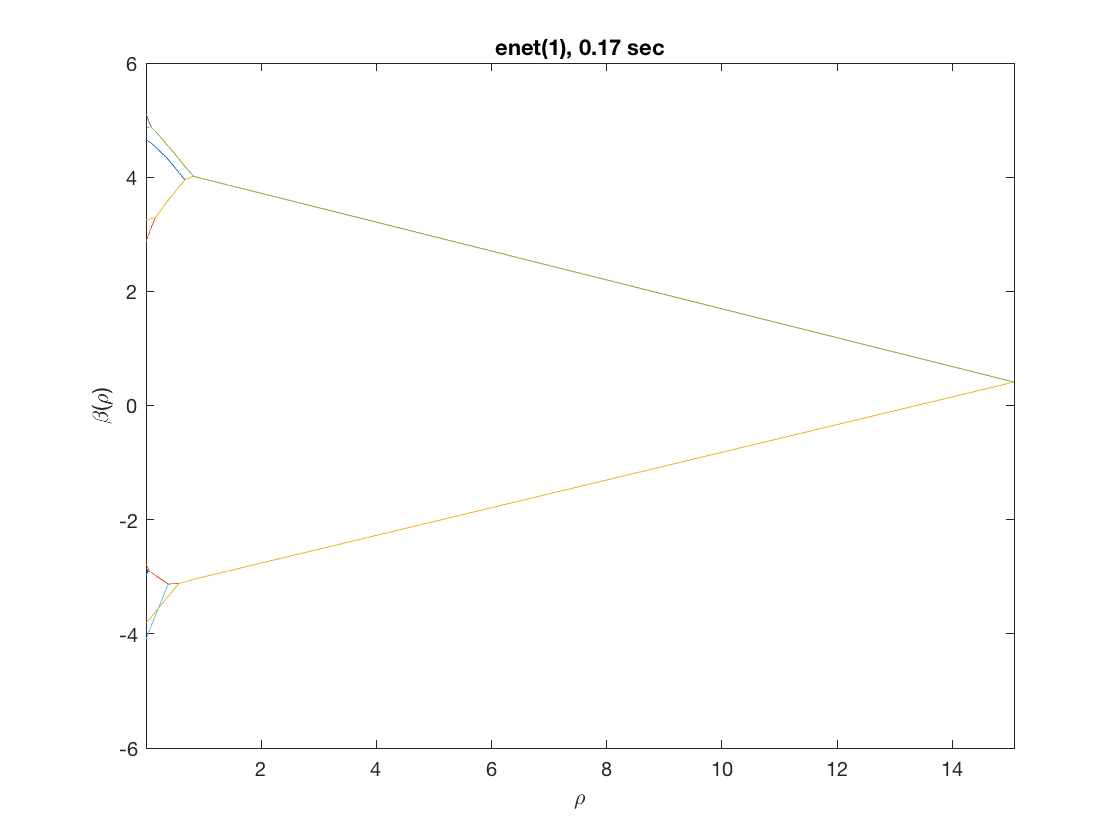
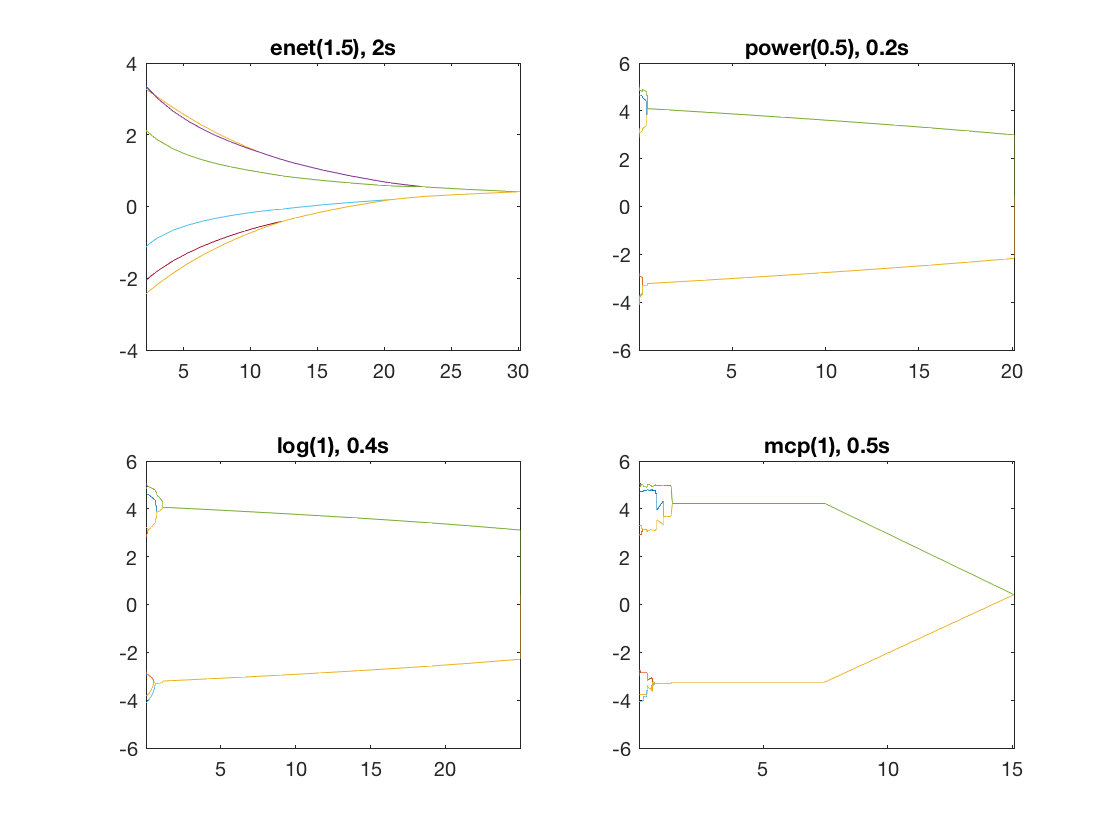
Same fusion problem, but with power, log, MCP, and SCAD penalty

penalty = {'enet' 'power' 'log' 'mcp'};
penparam = [1.5 0.5 1 1];
for i=1:length(penalty)
    tic;
    [rho_path, beta_path] = lsq_regpath(X,y,D,'penalty',penalty{i},...
        'penparam',penparam(i));
    timing = toc;
    subplot(2,2,i);
    plot(rho_path,beta_path(2:11,:));
    xlim([min(rho_path),max(rho_path)]);
    title([penalty{i} '(' num2str(penparam(i)) '), ' num2str(timing,1) 's']);
end

Sparse linear regression (n<p)

Simulate another sample data set (n=100, p=1000)

clear;
n = 100;
p = 1000;
X = randn(n,p);             % generate a random design matrix
X = bsxfun(@rdivide, X, sqrt(sum(X.^2,1))); % normalize predictors
X = [ones(size(X,1),1) X];  % add intercept
b = zeros(p+1,1);           % true signal
b(2:6) = 3;                 % first 5 predictors are 3
b(7:11) = -3;               % next 5 predictors are -3
y = X*b+randn(n,1);         % response vector

Solution path for lasso

maxpreds = 51;              % run solution path until 50 predictors are in
penalty = 'enet';           % set penalty function
penparam = 1;
penidx = [false; true(size(X,2)-1,1)];  % leave intercept unpenalized
tic;
[rho_path,beta_path,eb_path] = lsq_sparsepath(X,y,'penidx',penidx, ...
    'maxpreds',maxpreds,'penalty',penalty,'penparam',penparam);
timing = toc;
[~,ebidx] = min(eb_path);

figure;
plot(rho_path,eb_path);
xlabel('\rho');
ylabel('EBC');
xlim([min(rho_path),max(rho_path)]);
title([penalty '(' num2str(penparam) '), ' num2str(timing,2) ' sec']);
line([rho_path(ebidx), rho_path(ebidx)], ylim);

figure;
plot(rho_path,beta_path);
xlabel('\rho');
ylabel('\beta(\rho)');
xlim([min(rho_path),max(rho_path)]);
title([penalty '(' num2str(penparam) '), ' num2str(timing,2) ' sec']);
line([rho_path(ebidx), rho_path(ebidx)], ylim);

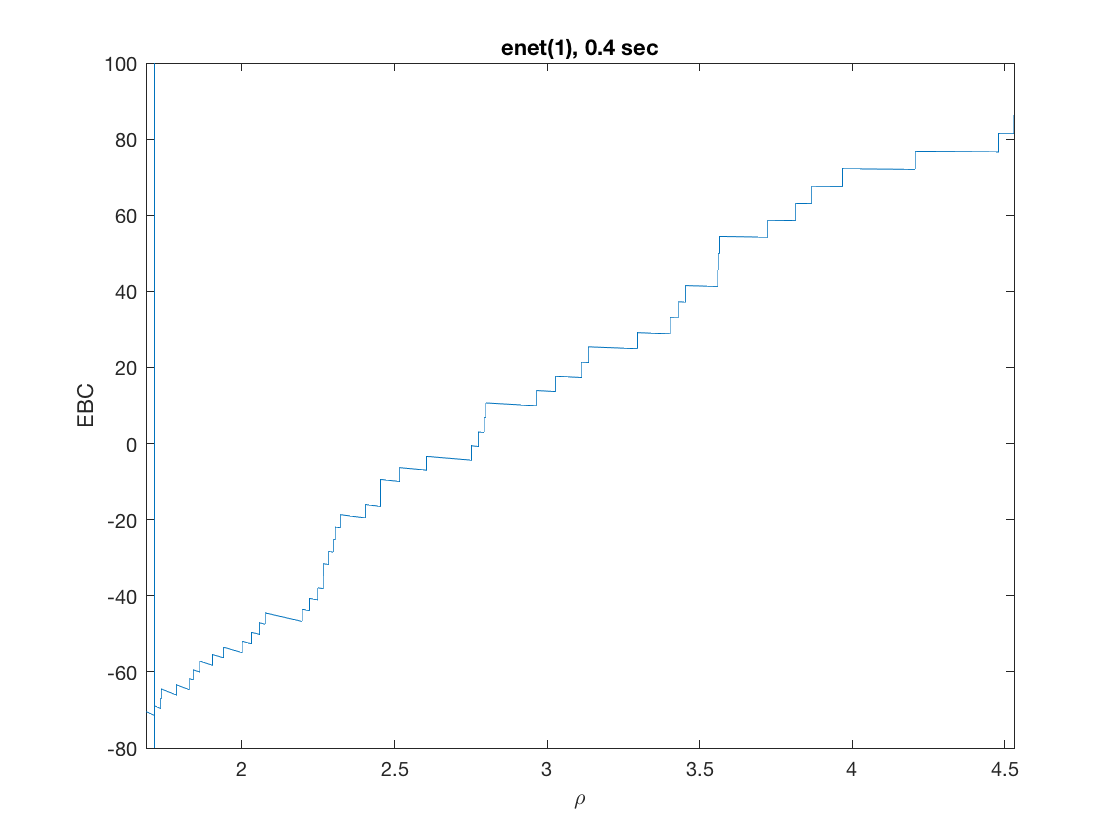
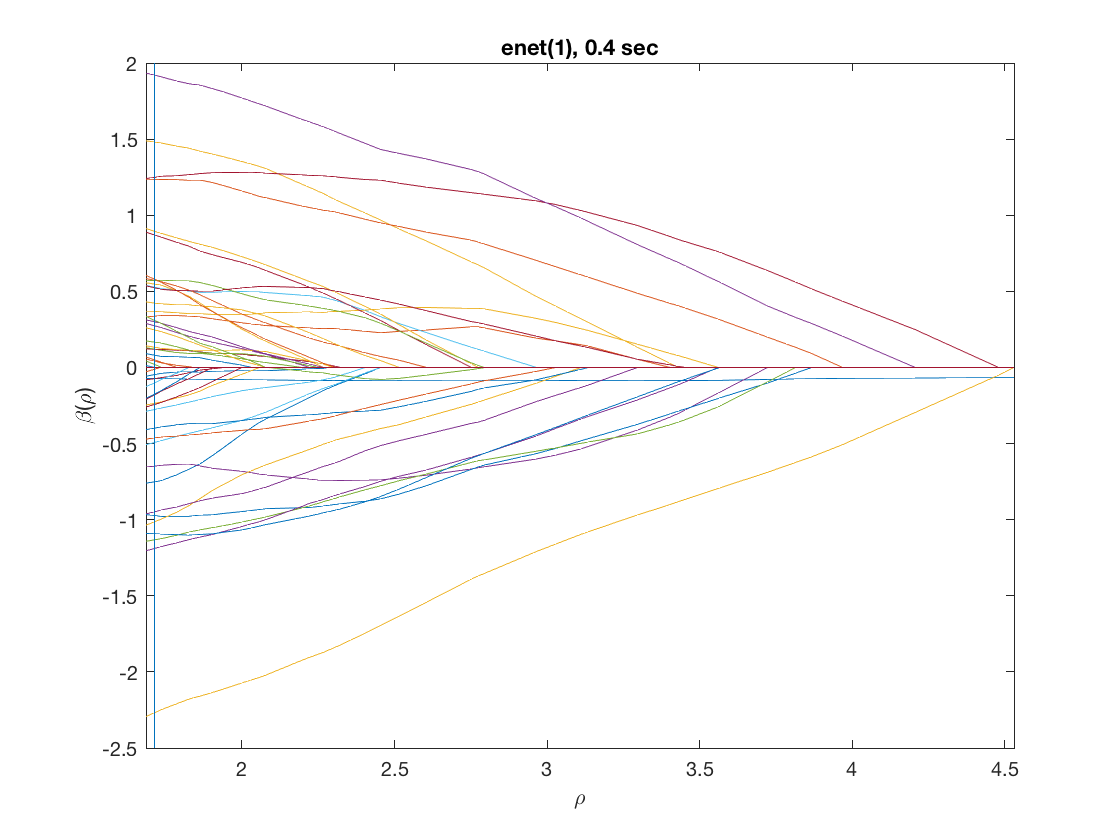
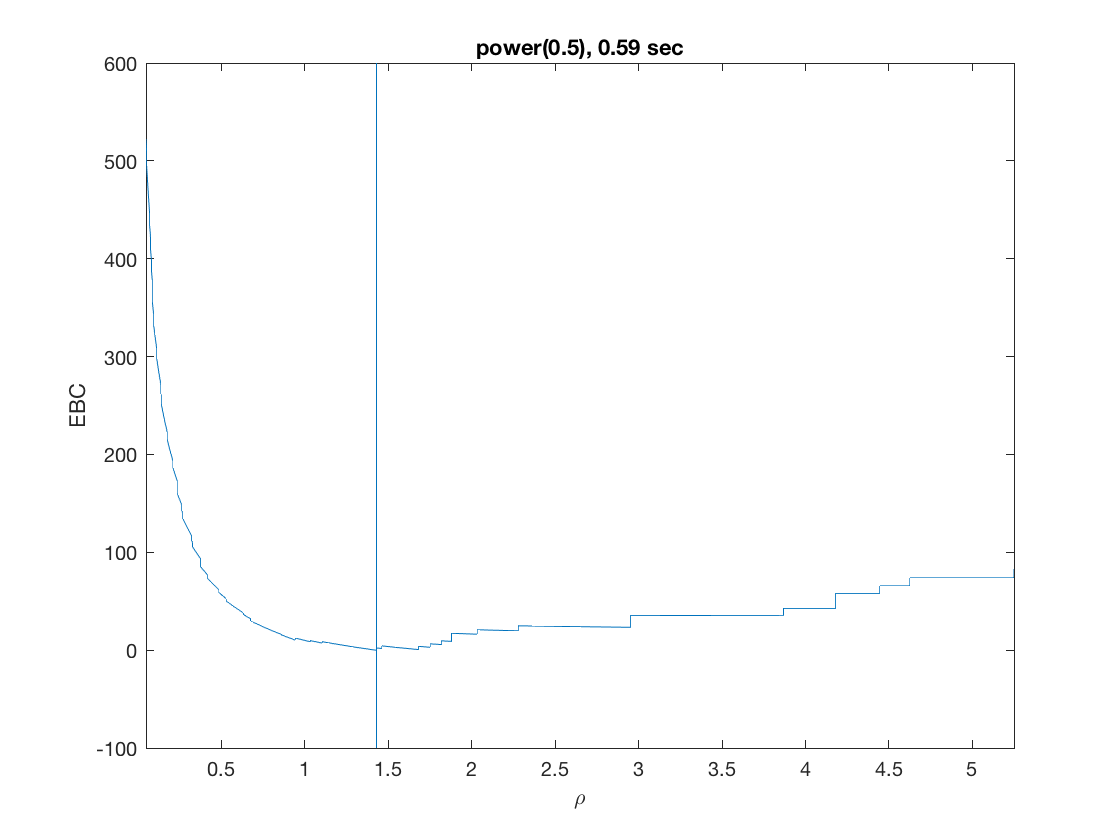
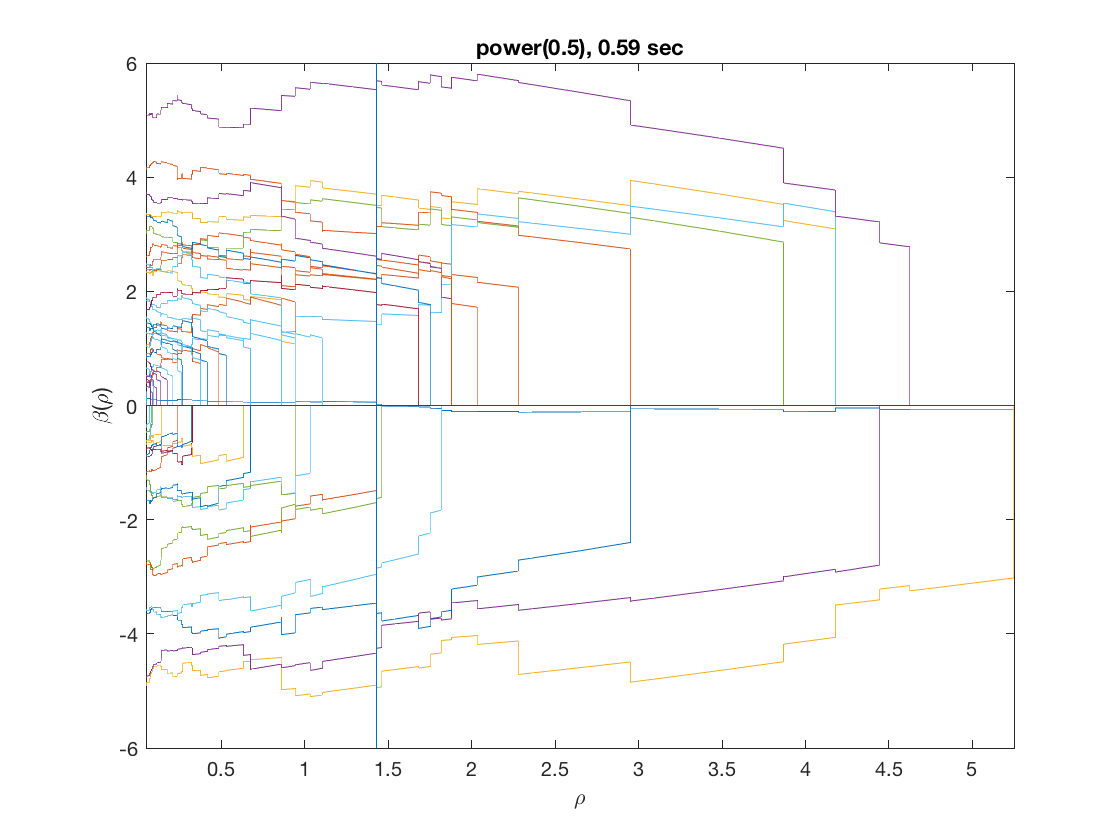
Solution path for power (0.5)

penalty = 'power';          % set penalty function to power
penparam = 0.5;
tic;
[rho_path,beta_path,eb_path] = lsq_sparsepath(X,y,'penidx',penidx, ...
    'maxpreds',maxpreds,'penalty',penalty,'penparam',penparam);
timing = toc;
[~,ebidx] = min(eb_path);

figure;
plot(rho_path,eb_path);
xlabel('\rho');
ylabel('EBC');
xlim([min(rho_path),max(rho_path)]);
title([penalty '(' num2str(penparam) '), ' num2str(timing,2) ' sec']);
line([rho_path(ebidx), rho_path(ebidx)], ylim);

figure;
plot(rho_path,beta_path);
xlabel('\rho');
ylabel('\beta(\rho)');
xlim([min(rho_path),max(rho_path)]);
title([penalty '(' num2str(penparam) '), ' num2str(timing,2) ' sec']);
line([rho_path(ebidx), rho_path(ebidx)], ylim);

Published with MATLAB® R2017a