Table of Contents¶
Introduction to Julia¶

Types of computer languages¶
Compiled languages: C/C++, Fortran, ...
- Directly compiled to machine code that is executed by CPU
- Pros: fast, memory efficient
- Cons: longer development time, hard to debug
Interpreted language: R, Matlab, Python, SAS IML, JavaScript, ...
- Interpreted by interpreter
- Pros: fast prototyping
- Cons: excruciatingly slow for loops
Mixed (dynamic) languages: Matlab (JIT), R (
compilerpackage), Julia, Cython, JAVA, ...- Pros and cons: between the compiled and interpreted languages
Script languages: Linux shell scripts, Perl, ...
- Extremely useful for some data preprocessing and manipulation
Database languages: SQL, Hive (Hadoop).
- Data analysis never happens if we do not know how to retrieve data from databases
Messages¶
To be versatile in the big data era, master at least one language in each category.
To improve efficiency of interpreted languages such as R or Matlab, conventional wisdom is to avoid loops as much as possible. Aka, vectorize code
The only loop you are allowed to have is that for an iterative algorithm.
When looping is unavoidable, need to code in C, C++, or Fortran.
Success stories: the popularglmnetpackage in R is coded in Fortran;tidyversepackages use a lot RCpp/C++.Modern languages such as Julia tries to solve the two language problem. That is to achieve efficiency without vectorizing code.
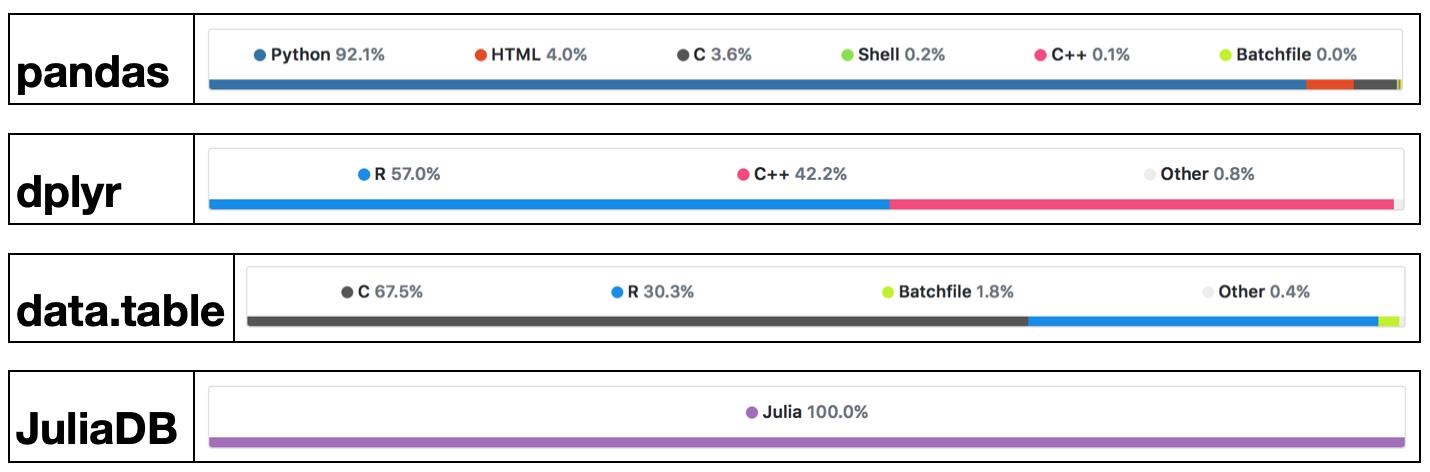
What's Julia?¶
Julia is a high-level, high-performance dynamic programming language for technical computing, with syntax that is familiar to users of other technical computing environments
History:
- Project started in 2009. First public release in 2012
- Creators: Jeff Bezanson, Alan Edelman, Stefan Karpinski, Viral Shah
- First major release v1.0 was released on Aug 8, 2018
- Current stable release v1.1.0
Aim to solve the notorious two language problem: Prototype code goes into high-level languages like R/Python, production code goes into low-level language like C/C++.
Julia aims to:
Walks like Python. Runs like C.
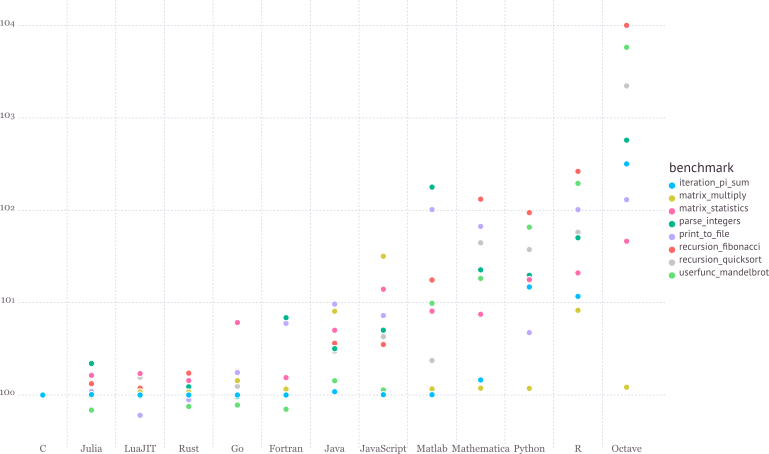
See https://julialang.org/benchmarks/ for the details of benchmark.
Write high-level, abstract code that closely resembles mathematical formulas
- yet produces fast, low-level machine code that has traditionally only been generated by static languages.
Julia is more than just "Fast R" or "Fast Matlab"
- Performance comes from features that work well together.
- You can't just take the magic dust that makes Julia fast and sprinkle it on [language of choice]
R is great, but...¶
It's not meant for high performance computing
- http://adv-r.had.co.nz/Performance.html
- Section on performance starts with "Why is R slow?"
- http://adv-r.had.co.nz/Performance.html
Deficiencies in the core language
- Many fixed with packages (
devtools,roxygen2,Matrix) - Others harder to fix (R uses an old version of BLAS)
- Some impossible to fix (clunky syntax, poor design choices)
- Many fixed with packages (
Only 6 active developers left (out of 20 R-Core members)
- JuliaLang organization has 75 members, with 567 total contributors (as of 3/3/17)
Doug Bates (member of R-Core,
Matrixandlme4)- Getting Doug on board was a big win for statistics with Julia, as he brought a lot of knowledge about the history of R development and design choices
https://github.com/dmbates/MixedModels.jl
As some of you may know, I have had a (rather late) mid-life crisis and run off with another language called Julia.
-- Doug Bates (on the `knitr` Google Group)
Gibbs sampler example by Doug Bates¶
An example from Dr. Doug Bates's slides Julia for R Programmers.
The task is to create a Gibbs sampler for the density
$$ f(x, y) = k x^2 exp(- x y^2 - y^2 + 2y - 4x), x > 0 $$ using the conditional distributions $$ \begin{eqnarray*} X | Y &\sim& \Gamma \left( 3, \frac{1}{y^2 + 4} \right) \\ Y | X &\sim& N \left(\frac{1}{1+x}, \frac{1}{2(1+x)} \right). \end{eqnarray*} $$
- R solution. The
RCall.jlpackage allows us to execute R code without leaving theJuliaenvironment. We first define an R functionRgibbs().
using RCall
R"""
library(Matrix)
Rgibbs <- function(N, thin) {
mat <- matrix(0, nrow=N, ncol=2)
x <- y <- 0
for (i in 1:N) {
for (j in 1:thin) {
x <- rgamma(1, 3, y * y + 4) # 3rd arg is rate
y <- rnorm(1, 1 / (x + 1), 1 / sqrt(2 * (x + 1)))
}
mat[i,] <- c(x, y)
}
mat
}
"""
To generate a sample of size 10,000 with a thinning of 500. How long does it take?
R"""
system.time(Rgibbs(10000, 500))
"""
- This is a Julia function for the simple Gibbs sampler:
using Distributions
function jgibbs(N, thin)
mat = zeros(N, 2)
x = y = 0.0
for i in 1:N
for j in 1:thin
x = rand(Gamma(3, 1 / (y * y + 4)))
y = rand(Normal(1 / (x + 1), 1 / sqrt(2(x + 1))))
end
mat[i, 1] = x
mat[i, 2] = y
end
mat
end
Generate the same number of samples. How long does it take?
jgibbs(100, 5); # warm-up
@elapsed jgibbs(10000, 500)
We see 40-80 fold speed up of Julia over R on this example, with similar coding effort!
Learning resources¶
YouTube: Intro to Julia (2h28m), by Jane Herriman.
Cheat sheet: The Fast Track to Julia.
Browse the Julia documentation.
For Matlab users, read Noteworthy Differences From Matlab.
For R users, read Noteworthy Differences From R.
For Python users, read Noteworthy Differences From Python.
The Learning page on Julia's website has pointers to many other learning resources.
Julia REPL (Read-Evaluation-Print-Loop)¶
The Julia REPL, or Julia shell, has at least five modes.
Default mode is the Julian prompt
julia>. Type backspace in other modes to enter default mode.Help mode
help?>. Type?to enter help mode.?search_termdoes a fuzzy search forsearch_term.Shell mode
shell>. Type;to enter shell mode.Package mode
v(1.1) Pkg>. Type]to enter package mode for managing Julia packages (install, uninstall, update, ...).Search mode
(reverse-i-search). Pressctrl+Rto enter search model.With
RCall.jlpackage installed, we can enter the R mode by typing$(shift+4) at Julia REPL.
Some survival commands in Julia REPL:
quit()orCtrl+D: exit Julia.Ctrl+C: interrupt execution.Ctrl+L: clear screen.Append
;(semi-colon) to suppress displaying output from a command. Same as Matlab.include("filename.jl")to source a Julia code file.
Seek help¶
Online help from REPL:
?function_name.Google (of course).
Julia documentation: https://docs.julialang.org/en/.
Look up source code:
@edit fun(x).Friends.
Which IDE?¶
Julia homepage lists many choices: Juno, VS Code, Vim, ...
Unfortunately at the moment there are no mature RStudio- or Matlab-like IDE for Julia yet.
For dynamic document, e.g., homework, I recommend Jupyter Notebook or JupyterLab. JupyterLab is supposed to replace Jupyter Notebook after it reaches v1.0.
For extensive Julia coding, myself has good experience with the editor VS Code with extensions
JuliaandVS Code Jupyter Notebook Previewerinstalled.
Julia package system¶
Each Julia package is a Git repository. Each Julia package name ends with
.jl. E.g.,Distributions.jlpackage lives at https://github.com/JuliaStats/Distributions.jl.
Google search withPackageName.jlusually leads to the package on github.com.The package ecosystem is rapidly maturing; a complete list of registered packages (which are required to have a certain level of testing and documentation) is at http://pkg.julialang.org/.
For example, the package called
Distributions.jlis added with# in Pkg mode (v1.1) pkg> add Distributions
and "removed" (although not completely deleted) with
# in Pkg mode (v1.1) pkg> rm Distributions
The package manager provides a dependency solver that determines which packages are actually required to be installed.
Non-registered packages are added by cloning the relevant Git repository. E.g.,
# in Pkg mode (v1.1) pkg> add https://github.com/OpenMendel/SnpArrays.jl
A package needs only be added once, at which point it is downloaded into your local
.julia/packagesdirectory in your home directory.
;ls ~/.julia/packages
- Directory of a specific package can be queried by
pathof():
using Distributions
pathof(Distributions)
If you start having problems with packages that seem to be unsolvable, you may try just deleting your .julia directory and reinstalling all your packages.
Periodically, one should run
updatein Pkg mode, which checks for, downloads and installs updated versions of all the packages you currently have installed.statuslists the status of all installed packages.Using functions in package.
using Distributions
This pulls all of the exported functions in the module into your local namespace, as you can check using the
whos()command. An alternative isimport Distributions
Now, the functions from the Distributions package are available only using
Distributions.<FUNNAME>
All functions, not only exported functions, are always available like this.
using RCall
x = randn(1000)
R"""
hist($x, main="I'm plotting a Julia vector")
"""
R"""
library(ggplot2)
qplot($x)
"""
x = R"""
rnorm(10)
"""
# collect R variable into Julia workspace
y = collect(x)
Access Julia variables in R REPL mode:
julia> x = rand(5) # Julia variable R> y <- $x
Pass Julia expression in R REPL mode:
R> y <- $(rand(5))
Put Julia variable into R environment:
julia> @rput x R> x
Get R variable into Julia environment:
R> r <- 2 Julia> @rget r
If you want to call Julia within R, check out the
XRJuliapackage by John Chambers.
Some basic Julia code¶
# an integer, same as int in R
y = 1
typeof(y)
# a Float64 number, same as double in R
y = 1.0
typeof(y)
# Greek letters: `\pi<tab>`
π
typeof(π)
# Greek letters: `\theta<tab>`
θ = y + π
# emoji! `\:kissing_cat:<tab>`
😽 = 5.0
# `\alpha<tab>\hat<tab>`
α̂ = π
# vector of Float64 0s
x = zeros(5)
# vector Int64 0s
x = zeros(Int, 5)
# matrix of Float64 0s
x = zeros(5, 3)
# matrix of Float64 1s
x = ones(5, 3)
# define array without initialization
x = Matrix{Float64}(undef, 5, 3)
# fill a matrix by 0s
fill!(x, 0)
# initialize an array to be constant 2.5
fill(2.5, (5, 3))
# rational number
a = 3//5
typeof(a)
b = 3//7
a + b
# uniform [0, 1) random numbers
x = rand(5, 3)
# uniform random numbers (in single precision)
x = rand(Float16, 5, 3)
# random numbers from {1,...,5}
x = rand(1:5, 5, 3)
# standard normal random numbers
x = randn(5, 3)
# range
1:10
typeof(1:10)
1:2:10
typeof(1:2:10)
# integers 1-10
x = collect(1:10)
# or equivalently
[1:10...]
# Float64 numbers 1-10
x = collect(1.0:10)
# convert to a specific type
convert(Vector{Float64}, 1:10)
Timing and benchmark¶
Julia¶
@time, @elapsed, @allocated macros:
using Random # standard library
Random.seed!(123) # seed
x = rand(1_000_000) # 1 million random numbers in [0, 1)
@time sum(x) # first run includes compilation time
@time sum(x) # no compilation time after first run
# just the runtime
@elapsed sum(x)
# just the allocation
@allocated sum(x)
Use package BenchmarkTools.jl for more robust benchmarking. Analog of microbenchmark package in R.
using BenchmarkTools
bm = @benchmark sum($x)
using Statistics # standard library
benchmark_result = Dict() # a dictionary to store median runtime (in milliseconds)
benchmark_result["Julia builtin"] = median(bm.times) / 1e6
C¶
We would use the low-level C code as the baseline for copmarison. In Julia, we can easily run compiled C code using the ccall function.
using Libdl
C_code = """
#include <stddef.h>
double c_sum(size_t n, double *X) {
double s = 0.0;
for (size_t i = 0; i < n; ++i) {
s += X[i];
}
return s;
}
"""
const Clib = tempname() # make a temporary file
# compile to a shared library by piping C_code to gcc
# (works only if you have gcc installed):
open(`gcc -std=c99 -fPIC -O3 -msse3 -xc -shared -o $(Clib * "." * Libdl.dlext) -`, "w") do f
print(f, C_code)
end
# define a Julia function that calls the C function:
c_sum(X::Array{Float64}) = ccall(("c_sum", Clib), Float64, (Csize_t, Ptr{Float64}), length(X), X)
# make sure it gives same answer
c_sum(x)
bm = @benchmark c_sum($x)
# store median runtime (in milliseconds)
benchmark_result["C"] = median(bm.times) / 1e6
R, buildin sum¶
Next we compare to the build in sum function in R, which is implemented using C.
using RCall
R"""
library(microbenchmark)
y <- $x
rbm <- microbenchmark(sum(y))
"""
# store median runtime (in milliseconds)
@rget rbm # dataframe
benchmark_result["R builtin"] = median(rbm[:time]) / 1e6
R, handwritten loop¶
Handwritten loop in R is much slower.
using RCall
R"""
sum_r <- function(x) {
s <- 0
for (xi in x) {
s <- s + xi
}
s
}
library(microbenchmark)
y <- $x
rbm <- microbenchmark(sum_r(y))
"""
# store median runtime (in milliseconds)
@rget rbm # dataframe
benchmark_result["R loop"] = median(rbm[:time]) / 1e6
Python, builtin sum¶
Built in function sum in Python.
using PyCall
PyCall.pyversion
# get the Python built-in "sum" function:
pysum = pybuiltin("sum")
bm = @benchmark $pysum($x)
# store median runtime (in miliseconds)
benchmark_result["Python builtin"] = median(bm.times) / 1e6
Python, handwritten loop¶
using PyCall
py"""
def py_sum(A):
s = 0.0
for a in A:
s += a
return s
"""
sum_py = py"py_sum"
bm = @benchmark $sum_py($x)
# store median runtime (in miliseconds)
benchmark_result["Python loop"] = median(bm.times) / 1e6
Python, numpy¶
Numpy is the high-performance scientific computing library for Python.
# bring in sum function from Numpy
numpy_sum = pyimport("numpy")."sum"
bm = @benchmark $numpy_sum($x)
# store median runtime (in miliseconds)
benchmark_result["Python numpy"] = median(bm.times) / 1e6
Numpy performance is on a par with Julia build-in sum function. Both are about 3 times faster than C, possibly because of usage of SIMD.
Summary¶
benchmark_result
CandR builtinare the baseline C performance (gold standard).Python builtinandPython loopare 80-100 fold slower than C because the loop is interpreted.R loopis about 30 folder slower than C and indicates the performance of bytecode generated by its compiler package (turned on by default since R v3.4.0 (Apr 2017)).Julia builtinandPython numpyare 3-4 folder faster than C because of SIMD (???).
Matrices and vectors¶
Dimensions¶
x = randn(5, 3)
size(x)
size(x, 1) # nrow() in R
size(x, 2)
# total number of elements
length(x)
Indexing¶
# 5 × 5 matrix of random Normal(0, 1)
x = randn(5, 5)
# first column
x[:, 1]
# first row
x[1, :]
# sub-array
x[1:2, 2:3]
# getting a subset of a matrix creates a copy, but you can also create "views"
z = view(x, 1:2, 2:3)
# same as
@views z = x[1:2, 2:3]
# change in z (view) changes x as well
z[2, 2] = 0.0
x
# y points to same data as x
y = x
# x and y point to same data
pointer(x), pointer(y)
# changing y also changes x
y[:, 1] .= 0
x
# create a new copy of data
z = copy(x)
pointer(x), pointer(z)
Concatenate matrices¶
# 1-by-3 array
[1 2 3]
# 3-by-1 vector
[1, 2, 3]
# multiple assignment by tuple
x, y, z = randn(5, 3), randn(5, 2), randn(3, 5)
[x y] # 5-by-5 matrix
[x y; z] # 8-by-5 matrix
Dot operation¶
Dot operation in Julia is elementwise operation, similar to Matlab.
x = randn(5, 3)
y = ones(5, 3)
x .* y # same x * y in R
x .^ (-2)
sin.(x)
Basic linear algebra¶
x = randn(5)
using LinearAlgebra
# vector L2 norm
norm(x)
# same as
sqrt(sum(abs2, x))
y = randn(5) # another vector
# dot product
dot(x, y) # x' * y
# same as
x'y
x, y = randn(5, 3), randn(3, 2)
# matrix multiplication, same as %*% in R
x * y
x = randn(3, 3)
# conjugate transpose
x'
b = rand(3)
x'b # same as x' * b
# trace
tr(x)
det(x)
rank(x)
Sparse matrices¶
using SparseArrays
# 10-by-10 sparse matrix with sparsity 0.1
X = sprandn(10, 10, .1)
# convert to dense matrix; be cautious when dealing with big data
Xfull = convert(Matrix{Float64}, X)
# convert a dense matrix to sparse matrix
sparse(Xfull)
# syntax for sparse linear algebra is same as dense linear algebra
β = ones(10)
X * β
# many functions apply to sparse matrices as well
sum(X)
Control flow and loops¶
- if-elseif-else-end
if condition1
# do something
elseif condition2
# do something
else
# do something
end
forloop
for i in 1:10
println(i)
end
- Nested
forloop:
for i in 1:10
for j in 1:5
println(i * j)
end
end
Same as
for i in 1:10, j in 1:5
println(i * j)
end
- Exit loop:
for i in 1:10
# do something
if condition1
break # skip remaining loop
end
end
- Exit iteration:
for i in 1:10
# do something
if condition1
continue # skip to next iteration
end
# do something
end
Functions¶
In Julia, all arguments to functions are passed by reference, in contrast to R and Matlab.
Function names ending with
!indicates that function mutates at least one argument, typically the first.sort!(x) # vs sort(x)
Function definition
function func(req1, req2; key1=dflt1, key2=dflt2)
# do stuff
return out1, out2, out3
end
Required arguments are separated with a comma and use the positional notation.
Optional arguments need a default value in the signature.
Semicolon is not required in function call.
return statement is optional.
Multiple outputs can be returned as a tuple, e.g., return out1, out2, out3.
Anonymous functions, e.g.,
x -> x^2, is commonly used in collection function or list comprehensions.map(x -> x^2, y) # square each element in x
Functions can be nested:
function outerfunction()
# do some outer stuff
function innerfunction()
# do inner stuff
# can access prior outer definitions
end
# do more outer stuff
end
- Functions can be vectorized using the Dot syntax:
function myfunc(x)
return sin(x^2)
end
x = randn(5, 3)
myfunc.(x)
Collection function (think this as the series of
applyfunctions in R).Apply a function to each element of a collection:
map(f, coll) # or
map(coll) do elem
# do stuff with elem
# must contain return
end
map(x -> sin(x^2), x)
map(x) do elem
elem = elem^2
return sin(elem)
end
# Mapreduce
mapreduce(x -> sin(x^2), +, x)
# same as
sum(x -> sin(x^2), x)
- List comprehension
[sin(2i + j) for i in 1:5, j in 1:3] # similar to Python
Type system¶
Every variable in Julia has a type.
When thinking about types, think about sets.
Everything is a subtype of the abstract type
Any.An abstract type defines a set of types
- Consider types in Julia that are a
Number:
- Consider types in Julia that are a
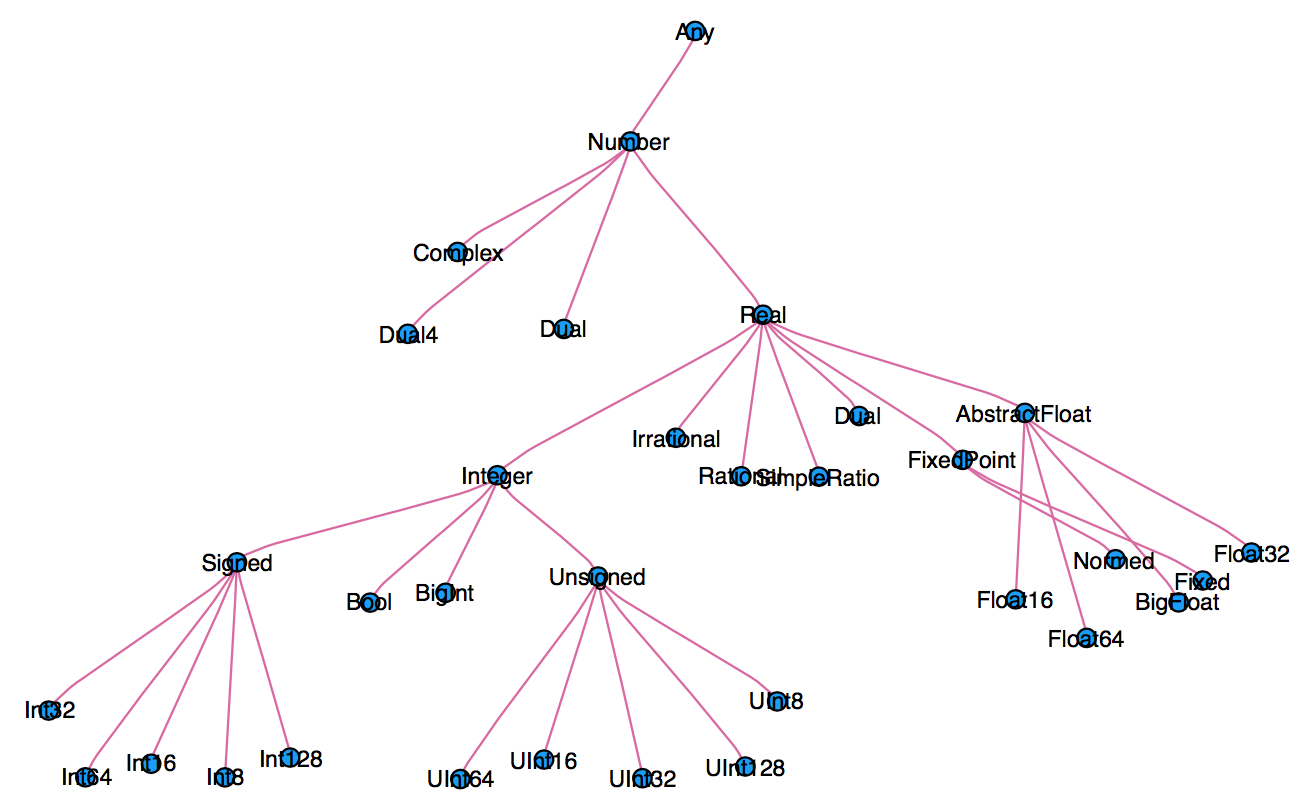
- We can explore type hierarchy with
typeof(),supertype(), andsubtypes().
typeof(1.0), typeof(1)
supertype(Float64)
subtypes(AbstractFloat)
# Is Float64 a subtype of AbstractFloat?
Float64 <: AbstractFloat
# On 64bit machine, Int == Int64
Int == Int64
# convert to Float64
convert(Float64, 1)
# same as
Float64(1)
# Float32 vector
x = randn(Float32, 5)
# convert to Float64
convert(Vector{Float64}, x)
# same as
Float64.(x)
# convert Float64 to Int64
convert(Int, 1.0)
convert(Int, 1.5) # should use round(1.5)
round(Int, 1.5)
Multiple dispatch¶
Multiple dispatch lies in the core of Julia design. It allows built-in and user-defined functions to be overloaded for different combinations of argument types.
Let's consider a simple "doubling" function:
g(x) = x + x
g(1.5)
This definition is too broad, since some things, e.g., strings, can't be added
g("hello world")
- This definition is correct but too restrictive, since any
Numbercan be added.
g(x::Float64) = x + x
- This definition will automatically work on the entire type tree above!
g(x::Number) = x + x
This is a lot nicer than
function g(x)
if isa(x, Number)
return x + x
else
throw(ArgumentError("x should be a number"))
end
end
methods(func)function display all methods defined forfunc.
methods(g)
When calling a function with multiple definitions, Julia will search from the narrowest signature to the broadest signature.
@which func(x)marco tells which method is being used for argument signaturex.
# an Int64 input
@which g(1)
# a Vector{Float64} input
@which g(randn(5))
Just-in-time compilation (JIT)¶
Following figures are taken from Arch D. Robinson's slides Introduction to Writing High Performance Julia.
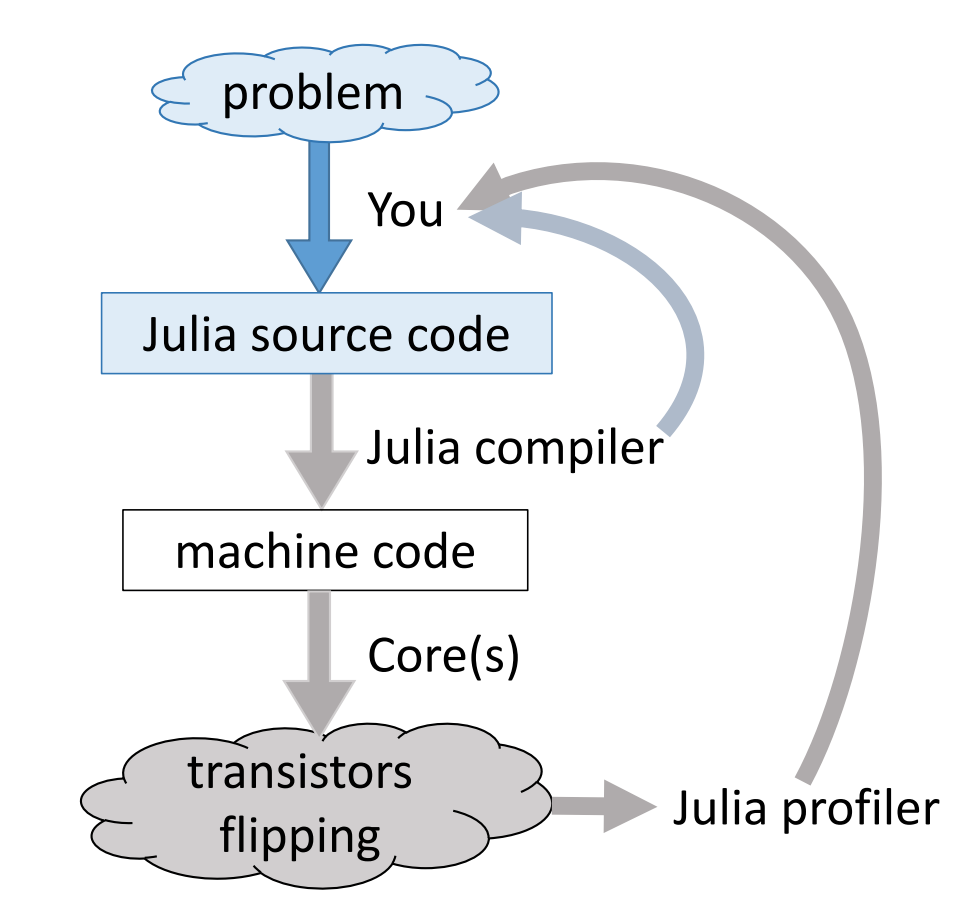 |
 |
|---|---|
Julia's efficiency results from its capability to infer the types of all variables within a function and then call LLVM to generate optimized machine code at run-time.
Consider the g (doubling) function defined earlier. This function will work on any type which has a method for +.
g(2), g(2.0)
Step 1: Parse Julia code into abstract syntax tree (AST).
@code_lowered g(2)
Step 2: Type inference according to input type.
@code_warntype g(2)
@code_warntype g(2.0)
Step 3: Compile into LLVM bytecode (equivalent of R bytecode generated by compiler package).
@code_llvm g(2)
@code_llvm g(2.0)
We didn't provide a type annotation. But different LLVM code gets generated depending on the argument type!
In R or Python, g(2) and g(2.0) would use the same code for both.
In Julia, g(2) and g(2.0) dispatches to optimized code for Int64 and Float64, respectively.
For integer input x, LLVM compiler is smart enough to know x + x is simple shifting x by 1 bit, which is faster than addition.
- Step 4: Lowest level is the assembly code, which is machine dependent.
@code_native g(2)
@code_native g(2.0)
Profiling Julia code¶
Julia has several built-in tools for profiling. The @time marco outputs run time and heap allocation.
# a function defined earlier
function tally(x::Array)
s = zero(eltype(x))
for v in x
s += v
end
s
end
using Random
Random.seed!(123)
a = rand(20_000_000)
@time tally(a) # first run: include compile time
@time tally(a)
For more robust benchmarking, the BenchmarkTools.jl package is highly recommended.
using BenchmarkTools
@benchmark tally($a)
The Profile module gives line by line profile results.
using Profile
Profile.clear()
@profile tally(a)
Profile.print(format=:flat)
One can use ProfileView package for better visualization of profile data:
using ProfileView
ProfileView.view()
Memory profiling¶
Detailed memory profiling requires a detour. First let's write a script bar.jl, which contains the workload function tally and a wrapper for profiling.
;cat bar.jl
Next, in terminal, we run the script with --track-allocation=user option.
;julia --track-allocation=user bar.jl
The profiler outputs a file bar.jl.21740.mem.
;cat bar.jl.21740.mem