Numerical linear algebra¶
System information (for reproducibility)
versioninfo()
Introduction¶
Topics in numerical algebra:
- BLAS
- solve linear equations $\mathbf{A} \mathbf{x} = \mathbf{b}$
- regression computations $\mathbf{X}^T \mathbf{X} \beta = \mathbf{X}^T \mathbf{y}$
- eigen-problems $\mathbf{A} \mathbf{x} = \lambda \mathbf{x}$
- generalized eigen-problems $\mathbf{A} \mathbf{x} = \lambda \mathbf{B} \mathbf{x}$
- singular value decompositions $\mathbf{A} = \mathbf{U} \Sigma \mathbf{V}^T$
- iterative methods for numerical linear algebra
Except for the iterative methods, most of these numerical linear algebra tasks are implemented in the BLAS and LAPACK libraries. They form the building blocks of most statistical computing tasks (optimization, MCMC).
All high-level languages (R, Matlab, Julia) call BLAS and LAPACK for numerical linear algebra.
- Julia offers more flexibility by exposing interfaces to many BLAS/LAPACK subroutines directly. See documentation.
BLAS¶
BLAS stands for basic linear algebra subprograms.
See netlib for a complete list of standardized BLAS functions.
There are many implementations of BLAS.
There are 3 levels of BLAS functions.
| Level | Example Operation | Name | Dimension | Flops |
|---|---|---|---|---|
| 1 | $\alpha \gets \mathbf{x}^T \mathbf{y}$ | dot product | $\mathbf{x}, \mathbf{y} \in \mathbb{R}^n$ | $2n$ |
| 1 | $\mathbf{y} \gets \mathbf{y} + \alpha \mathbf{x}$ | axpy | $\alpha \in \mathbb{R}$, $\mathbf{x}, \mathbf{y} \in \mathbb{R}^n$ | $2n$ |
| 2 | $\mathbf{y} \gets \mathbf{y} + \mathbf{A} \mathbf{x}$ | gaxpy | $\mathbf{A} \in \mathbb{R}^{m \times n}$, $\mathbf{x} \in \mathbb{R}^n$, $\mathbf{y} \in \mathbb{R}^m$ | $2mn$ |
| 2 | $\mathbf{A} \gets \mathbf{A} + \mathbf{y} \mathbf{x}^T$ | rank one update | $\mathbf{A} \in \mathbb{R}^{m \times n}$, $\mathbf{x} \in \mathbb{R}^n$, $\mathbf{y} \in \mathbb{R}^m$ | $2mn$ |
| 3 | $\mathbf{C} \gets \mathbf{C} + \mathbf{A} \mathbf{B}$ | matrix multiplication | $\mathbf{A} \in \mathbb{R}^{m \times p}$, $\mathbf{B} \in \mathbb{R}^{p \times n}$, $\mathbf{C} \in \mathbb{R}^{m \times n}$ | $2mnp$ |
- Typical BLAS functions support single precision (S), double precision (D), complex (C), and double complex (Z).
Examples¶
The form of a mathematical expression and the way the expression should be evaluated in actual practice may be quite different.
Some operations appear as level-3 but indeed are level-2.
Example 1. A common operation in statistics is column scaling or row scaling
$$
\begin{eqnarray*}
\mathbf{A} &=& \mathbf{A} \mathbf{D} \quad \text{(column scaling)} \\
\mathbf{A} &=& \mathbf{D} \mathbf{A} \quad \text{(row scaling)},
\end{eqnarray*}
$$
where $\mathbf{D}$ is diagonal. For example, in generalized linear models (GLMs), the Fisher information matrix takes the form
$$
\mathbf{X}^T \mathbf{W} \mathbf{X},
$$
where $\mathbf{W}$ is a diagonal matrix with observation weights on diagonal.
Column and row scalings are essentially level-2 operations!
using BenchmarkTools, LinearAlgebra, Random
Random.seed!(123) # seed
n = 2000
A = rand(n, n) # n-by-n matrix
d = rand(n) # n vector
D = Diagonal(d) # diagonal matrix with d as diagonal
Dfull = convert(Matrix, D) # convert to full matrix
# this is calling BLAS routine for matrix multiplication: O(n^3) flops
# this is SLOW!
@benchmark $A * $Dfull
# dispatch to special method for diagonal matrix multiplication.
# columnwise scaling: O(n^2) flops
@benchmark $A * $D
# in-place: avoid allocate space for result
# rmul!: compute matrix-matrix product AB, overwriting A, and return the result.
@benchmark rmul!($A, $D)
Note: In R or Matlab, diag(d) will create a full matrix. Be cautious using diag function: do we really need a full diagonal matrix?
using RCall
R"""
d <- runif(5)
diag(d)
"""
Example 2. Innter product between two matrices $\mathbf{A}, \mathbf{B} \in \mathbb{R}^{m \times n}$ is often written as $$ \text{trace}(\mathbf{A}^T \mathbf{B}), \text{trace}(\mathbf{B} \mathbf{A}^T), \text{trace}(\mathbf{A} \mathbf{B}^T), \text{ or } \text{trace}(\mathbf{B}^T \mathbf{A}). $$ They appear as level-3 operation (matrix multiplication with $O(m^2n)$ or $O(mn^2)$ flops).
Random.seed!(123)
n = 2000
A, B = randn(n, n), randn(n, n)
# slow way to evaluate this thing
@benchmark tr(transpose($A) * $B)
But $\text{trace}(\mathbf{A}^T \mathbf{B}) = <\text{vec}(\mathbf{A}), \text{vec}(\mathbf{B})>$. The latter is level-2 operation with $O(mn)$ flops.
@benchmark dot($A, $B)
Example 3. Similarly $\text{diag}(\mathbf{A}^T \mathbf{B})$ can be calculated in $O(mn)$ flops.
# slow way to evaluate this thing: O(n^3)
@benchmark diag(transpose($A) * $B)
# smarter: O(n^2)
@benchmark Diagonal(vec(sum($A .* $B, dims=1)))
To get rid of allocation of intermediate array at all, we can just write a double loop or use dot function.
using LoopVectorization
function diag_matmul!(d, A, B)
m, n = size(A)
@assert size(B) == (m, n) "A and B should have same size"
fill!(d, 0)
@avx for j in 1:n, i in 1:m
d[j] += A[i, j] * B[i, j]
end
# for j in 1:n
# @views d[j] = dot(A[:, j], B[:, j])
# end
Diagonal(d)
end
d = zeros(eltype(A), size(A, 2))
@benchmark diag_matmul!($d, $A, $B)
Memory hierarchy and level-3 fraction¶
Key to high performance is effective use of memory hierarchy. True on all architectures.
- Flop count is not the sole determinant of algorithm efficiency. Another important factor is data movement through the memory hierarchy.


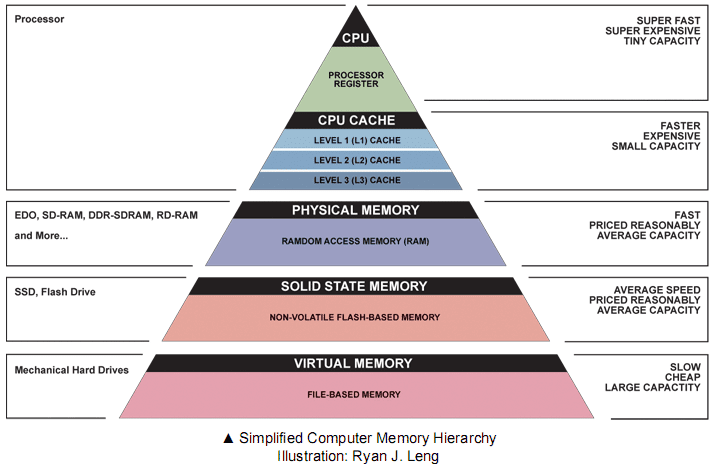
- Numbers everyone should know
| Operation | Time |
|---|---|
| L1 cache reference | 0.5 ns |
| L2 cache reference | 7 ns |
| Main memory reference | 100 ns |
| Read 1 MB sequentially from memory | 250,000 ns |
| Read 1 MB sequentially from SSD | 1,000,000 ns |
| Read 1 MB sequentially from disk | 20,000,000 ns |
Source: https://gist.github.com/jboner/2841832
For example, Xeon X5650 CPU has a theoretical throughput of 128 DP GFLOPS but a max memory bandwidth of 32GB/s.
Can we keep CPU cores busy with enough deliveries of matrix data and ship the results to memory fast enough to avoid backlog?
Answer: use high-level BLAS as much as possible.
| BLAS | Dimension | Mem. Refs. | Flops | Ratio |
|---|---|---|---|---|
| Level 1: $\mathbf{y} \gets \mathbf{y} + \alpha \mathbf{x}$ | $\mathbf{x}, \mathbf{y} \in \mathbb{R}^n$ | $3n$ | $2n$ | 3:2 |
| Level 2: $\mathbf{y} \gets \mathbf{y} + \mathbf{A} \mathbf{x}$ | $\mathbf{x}, \mathbf{y} \in \mathbb{R}^n$, $\mathbf{A} \in \mathbb{R}^{n \times n}$ | $n^2$ | $2n^2$ | 1:2 |
| Level 3: $\mathbf{C} \gets \mathbf{C} + \mathbf{A} \mathbf{B}$ | $\mathbf{A}, \mathbf{B}, \mathbf{C} \in\mathbb{R}^{n \times n}$ | $4n^2$ | $2n^3$ | 2:n |
- Higher level BLAS (3 or 2) make more effective use of arithmetic logic units (ALU) by keeping them busy. Surface-to-volume effect.
See Dongarra slides.
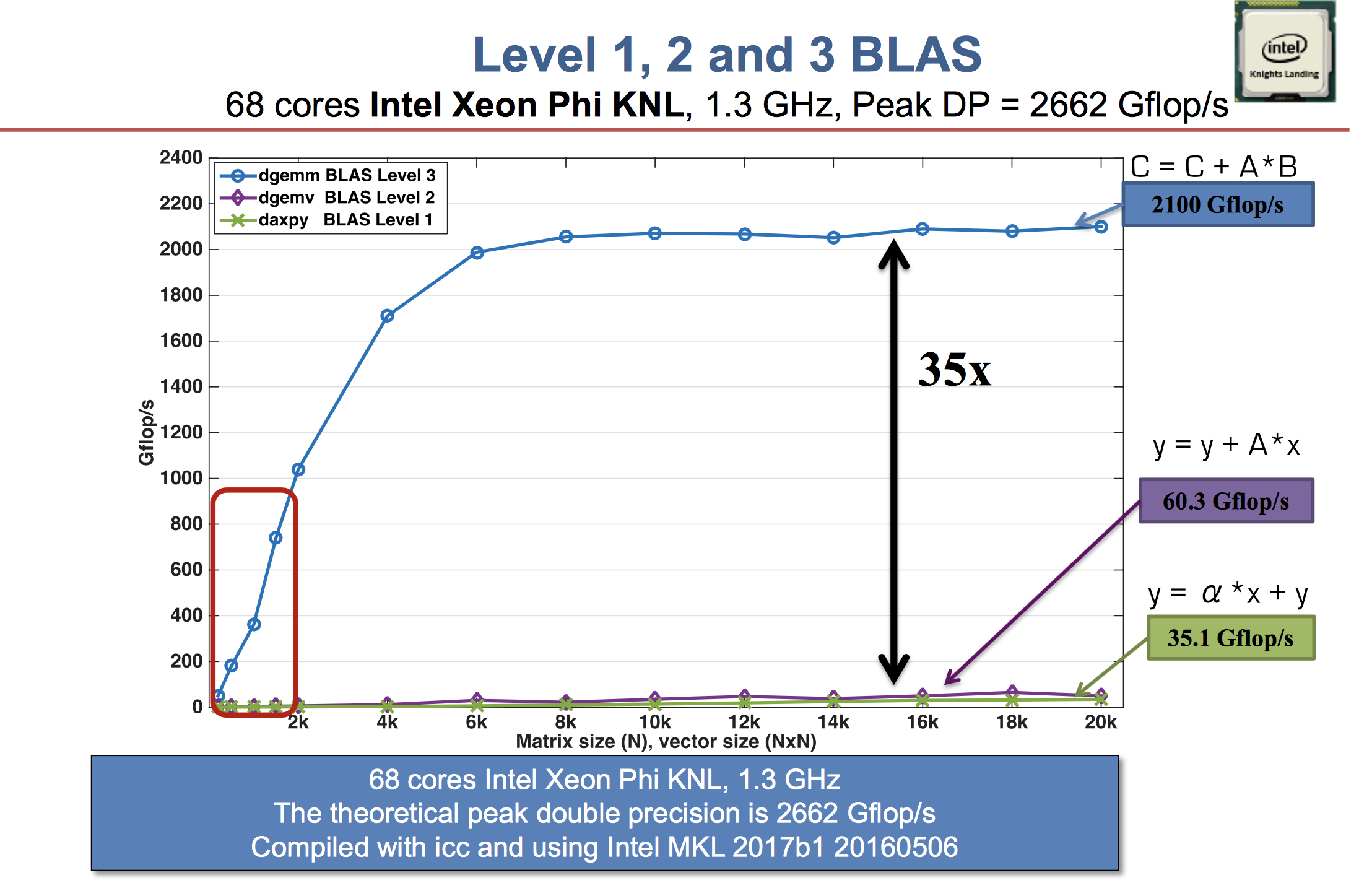
A distinction between LAPACK and LINPACK (older version of R uses LINPACK) is that LAPACK makes use of higher level BLAS as much as possible (usually by smart partitioning) to increase the so-called level-3 fraction.
To appreciate the efforts in an optimized BLAS implementation such as OpenBLAS (evolved from GotoBLAS), see the Quora question, especially the video. Bottomline is
Get familiar with (good implementations of) BLAS/LAPACK and use them as much as possible.
Effect of data layout¶
Data layout in memory affects algorithmic efficiency too. It is much faster to move chunks of data in memory than retrieving/writing scattered data.
Storage mode: column-major (Fortran, Matlab, R, Julia) vs row-major (C/C++).
Cache line is the minimum amount of cache which can be loaded and stored to memory.
- x86 CPUs: 64 bytes
- ARM CPUs: 32 bytes
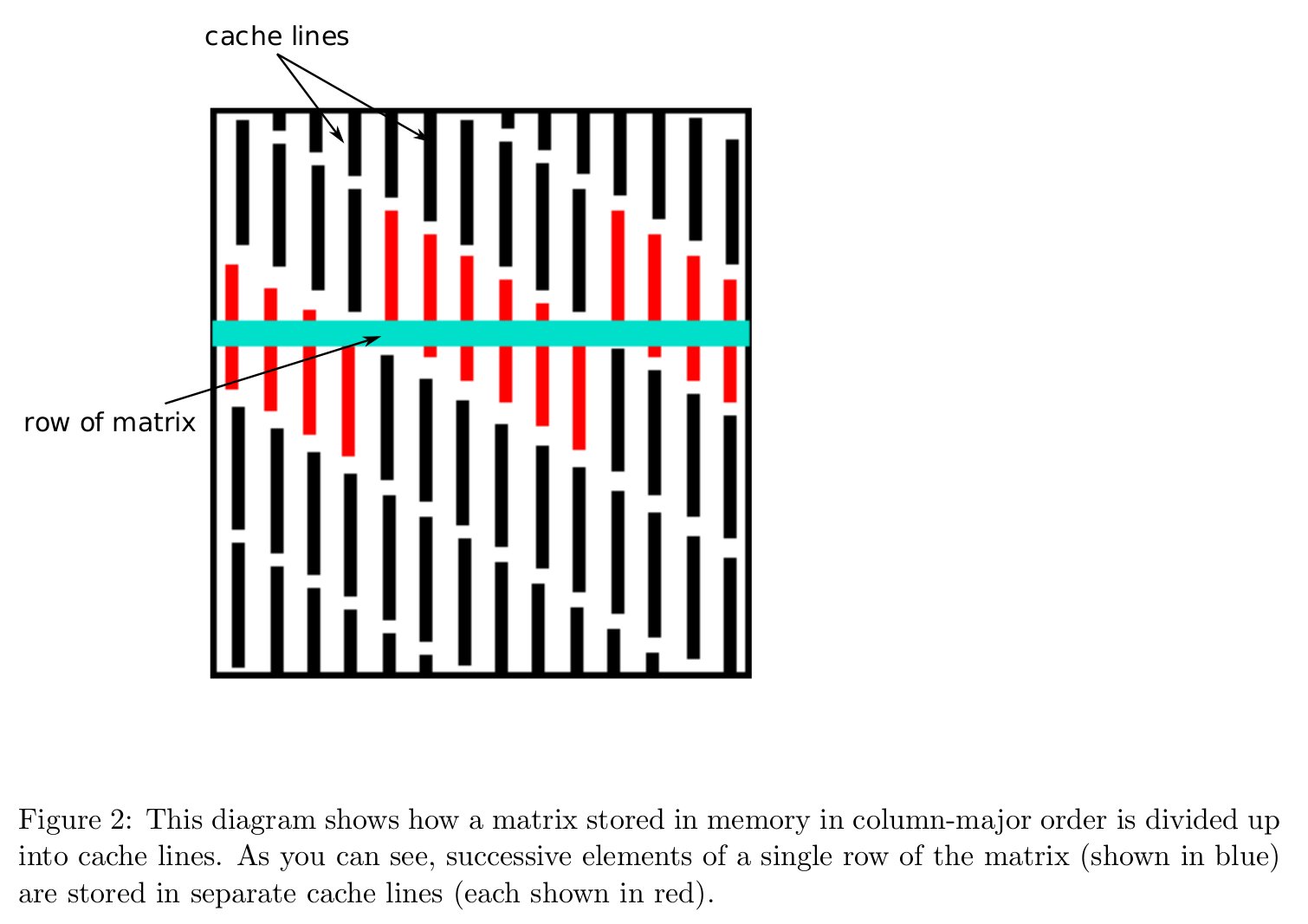
Accessing column-major stored matrix by rows ($ij$ looping) causes lots of cache misses.
Take matrix multiplication as an example $$ \mathbf{C} \gets \mathbf{C} + \mathbf{A} \mathbf{B}, \quad \mathbf{A} \in \mathbb{R}^{m \times p}, \mathbf{B} \in \mathbb{R}^{p \times n}, \mathbf{C} \in \mathbb{R}^{m \times n}. $$ Assume the storage is column-major, such as in Julia. There are 6 variants of the algorithms according to the order in the triple loops.
jkiorkjilooping:# inner most loop for i = 1:m C[i, j] = C[i, j] + A[i, k] * B[k, j] end
ikjorkijlooping:# inner most loop for j = 1:n C[i, j] = C[i, j] + A[i, k] * B[k, j] end
ijkorjiklooping:# inner most loop for k = 1:p C[i, j] = C[i, j] + A[i, k] * B[k, j] end
- We pay attention to the innermost loop, where the vector calculation occurs. The associated stride when accessing the three matrices in memory (assuming column-major storage) is
| Variant | A Stride | B Stride | C Stride |
|---|---|---|---|
| $jki$ or $kji$ | Unit | 0 | Unit |
| $ikj$ or $kij$ | 0 | Non-Unit | Non-Unit |
| $ijk$ or $jik$ | Non-Unit | Unit | 0 |
Apparently the variants $jki$ or $kji$ are preferred.
"""
matmul_by_loop!(A, B, C, order)
Overwrite `C` by `A * B`. `order` indicates the looping order for triple loop.
"""
function matmul_by_loop!(A::Matrix, B::Matrix, C::Matrix, order::String)
m = size(A, 1)
p = size(A, 2)
n = size(B, 2)
fill!(C, 0)
if order == "jki"
@inbounds for j = 1:n, k = 1:p, i = 1:m
C[i, j] += A[i, k] * B[k, j]
end
end
if order == "kji"
@inbounds for k = 1:p, j = 1:n, i = 1:m
C[i, j] += A[i, k] * B[k, j]
end
end
if order == "ikj"
@inbounds for i = 1:m, k = 1:p, j = 1:n
C[i, j] += A[i, k] * B[k, j]
end
end
if order == "kij"
@inbounds for k = 1:p, i = 1:m, j = 1:n
C[i, j] += A[i, k] * B[k, j]
end
end
if order == "ijk"
@inbounds for i = 1:m, j = 1:n, k = 1:p
C[i, j] += A[i, k] * B[k, j]
end
end
if order == "jik"
@inbounds for j = 1:n, i = 1:m, k = 1:p
C[i, j] += A[i, k] * B[k, j]
end
end
end
using Random
Random.seed!(123)
m, p, n = 2000, 100, 2000
A = rand(m, p)
B = rand(p, n)
C = zeros(m, n);
- $jki$ and $kji$ looping:
using BenchmarkTools
@benchmark matmul_by_loop!($A, $B, $C, "jki")
@benchmark matmul_by_loop!($A, $B, $C, "kji")
- $ikj$ and $kij$ looping:
@benchmark matmul_by_loop!($A, $B, $C, "ikj")
@benchmark matmul_by_loop!($A, $B, $C, "kij")
- $ijk$ and $jik$ looping:
@benchmark matmul_by_loop!($A, $B, $C, "ijk")
@benchmark matmul_by_loop!($A, $B, $C, "ijk")
- Julia wraps BLAS library for matrix multiplication. We see BLAS library wins hands down (multi-threading, Strassen algorithm, higher level-3 fraction by block outer product).
@benchmark mul!($C, $A, $B)
# direct call of BLAS wrapper function
@benchmark LinearAlgebra.BLAS.gemm!('N', 'N', 1.0, $A, $B, 0.0, $C)
Exercise: Annotate the loop in matmul_by_loop! by @avx and benchmark again.
BLAS in R¶
- Tip for R user. Standard R distribution from CRAN uses a very out-dated BLAS/LAPACK library.
using RCall
R"""
library(dplyr)
library(bench)
bench::mark($A %*% $B) %>%
print(width = Inf)
""";
Re-build R from source using OpenBLAS or MKL will immediately boost linear algebra performance in R. Google
build R using MKLto get started. Similarly we can build Julia using MKL.Matlab uses MKL. Usually it's very hard to beat Matlab in terms of linear algebra.
Avoid memory allocation: some examples¶
- Transposing matrix is an expensive memory operation.
- In R, the command will first transpose
t(A) %*% x
Athen perform matrix multiplication, causing unnecessary memory allocation - Julia is smart to avoid transposing matrix if possible.
- In R, the command
using Random, LinearAlgebra, BenchmarkTools
Random.seed!(123)
n = 1000
A = rand(n, n)
x = rand(n);
typeof(transpose(A))
fieldnames(typeof(transpose(A)))
# same data in tranpose(A) and original matrix A
pointer(transpose(A).parent), pointer(A)
# dispatch to BLAS
# does *not* actually transpose the matrix
@benchmark transpose($A) * $x
# pre-allocate result
out = zeros(size(A, 2))
@benchmark mul!($out, transpose($A), $x)
# or call BLAS wrapper directly
@benchmark LinearAlgebra.BLAS.gemv!('T', 1.0, $A, $x, 0.0, $out)
Broadcasting in Julia achieves vectorized code without creating intermediate arrays.
Suppose we want to calculate elementsize maximum of absolute values of two large arrays. In R or Matlab, the command
max(abs(X), abs(Y))
will create two intermediate arrays and then one result array.
using RCall
Random.seed!(123)
X, Y = rand(1000, 1000), rand(1000, 1000)
R"""
library(dplyr)
library(bench)
bench::mark(max(abs($X), abs($Y))) %>%
print(width = Inf)
""";
In Julia, dot operations are fused so no intermediate arrays are created.
# no intermediate arrays created, only result array created
@benchmark max.(abs.($X), abs.($Y))
Pre-allocating result array gets rid of memory allocation at all.
# no memory allocation at all!
Z = zeros(size(X)) # zero matrix of same size as X
@benchmark $Z .= max.(abs.($X), abs.($Y)) # .= (vs =) is important!
- View-1) avoids creating extra copy of matrix data.
Random.seed!(123)
A = randn(1000, 1000)
# sum entries in a sub-matrix
@benchmark sum($A[1:2:500, 1:2:500])
# view avoids creating a separate sub-matrix
@benchmark sum(@view $A[1:2:500, 1:2:500])
The @views macro, which can be useful in some operations.
@benchmark @views sum($A[1:2:500, 1:2:500])