Contents

Tucker linear regression, 2D covariates

clear;
% reset random seed
s = RandStream('mt19937ar','Seed',2);
RandStream.setGlobalStream(s);

True coefficients for regular (non-array) covariates

p0 = 5;
b0 = ones(p0,1);

2D true signal: 64-by-64 cross

shape = imread('cross.gif');
shape = array_resize(shape,[32,32]); % 32-by-32
b = zeros(2*size(shape));
b((size(b,1)/4):(size(b,1)/4)+size(shape,1)-1, ...
    (size(b,2)/4):(size(b,2)/4)+size(shape,2)-1) = shape;
[p1,p2] = size(b);
disp(size(b));

    64    64

Simulate covariates

n = 500;    % sample size
X = randn(n,p0);   % n-by-p0 regular design matrix
M = tensor(randn(p1,p2,n));  % p1-by-p2-by-n matrix variates
disp(size(M));

    64    64   500

Simulate responses

mu = X*b0 + double(ttt(tensor(b), M, 1:2));
sigma = 1;  % noise level
y = mu + sigma*randn(n,1);

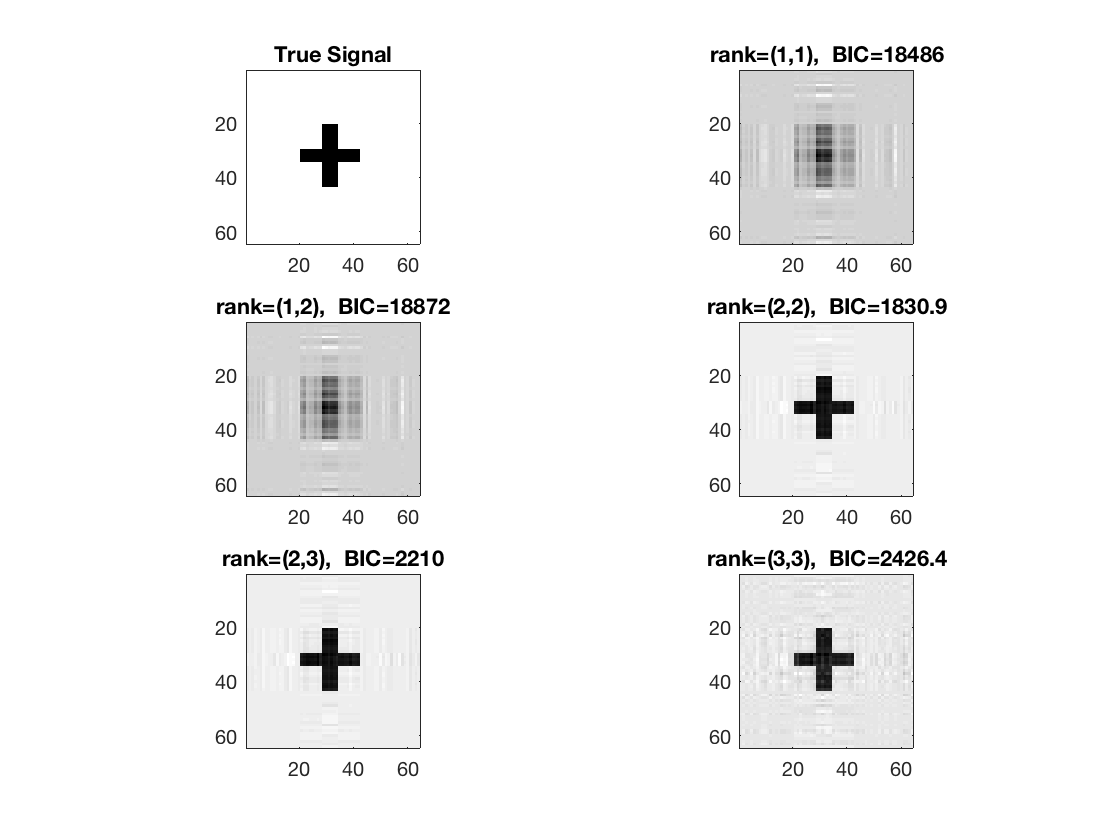
Estimate using Tucker linear regression - rank (1 1)

tic;
disp('rank (1 1)');
[~,beta_rk1,glmstats1] = tucker_reg(X,M,y,[1 1],'normal');
toc;

rank (1 1)
Elapsed time is 1.184909 seconds.

Estimate using Tucker linear regression - rank (1 2)

tic;
disp('rank (1 2)');
[~,beta_rk12,glmstats12] = tucker_reg(X,M,y,[1 2],'normal');
toc;

rank (1 2)
Elapsed time is 1.525358 seconds.

Estimate using Tucker linear regression - rank (2 2)

tic;
disp('rank (2 2)');
[~,beta_rk2,glmstats2] = tucker_reg(X,M,y,[2 2],'normal');
toc;

rank (2 2)
Elapsed time is 2.314233 seconds.

Estimate using Tucker linear regression - rank (2 3)

tic;
disp('rank (2 3)');
[~,beta_rk23,glmstats23] = tucker_reg(X,M,y,[2 3],'normal');
toc;

rank (2 3)
Elapsed time is 2.528255 seconds.

Estimate using Tucker linear regression - rank (3 3)

tic;
disp('rank (3 3)');
[~,beta_rk3,glmstats3,dev3] = tucker_reg(X,M,y,[3 3],'normal');
toc;

rank (3 3)
Elapsed time is 11.935729 seconds.

disp true and recovered signals

figure; hold on;
set(gca,'FontSize',20);

subplot(3,2,1);
imagesc(-b);
colormap(gray);
title('True Signal');
axis equal;
axis tight;

subplot(3,2,2);
imagesc(-double(beta_rk1));
colormap(gray);
title({['rank=(1,1), ', ' BIC=',num2str(glmstats1{end}.BIC,5)]});
axis equal;
axis tight;

subplot(3,2,3);
imagesc(-double(beta_rk12));
colormap(gray);
title({['rank=(1,2), ', ' BIC=',num2str(glmstats12{end}.BIC,5)]});
axis equal;
axis tight;

subplot(3,2,4);
imagesc(-double(beta_rk2));
colormap(gray);
title({['rank=(2,2), ', ' BIC=',num2str(glmstats2{end}.BIC,5)]});
axis equal;
axis tight;

subplot(3,2,5);
imagesc(-double(beta_rk23));
colormap(gray);
title({['rank=(2,3), ', ' BIC=',num2str(glmstats23{end}.BIC,5)]});
axis equal;
axis tight;

subplot(3,2,6);
imagesc(-double(beta_rk3));
colormap(gray);
title({['rank=(3,3), ', ' BIC=',num2str(glmstats3{end}.BIC,5)]});
axis equal;
axis tight;

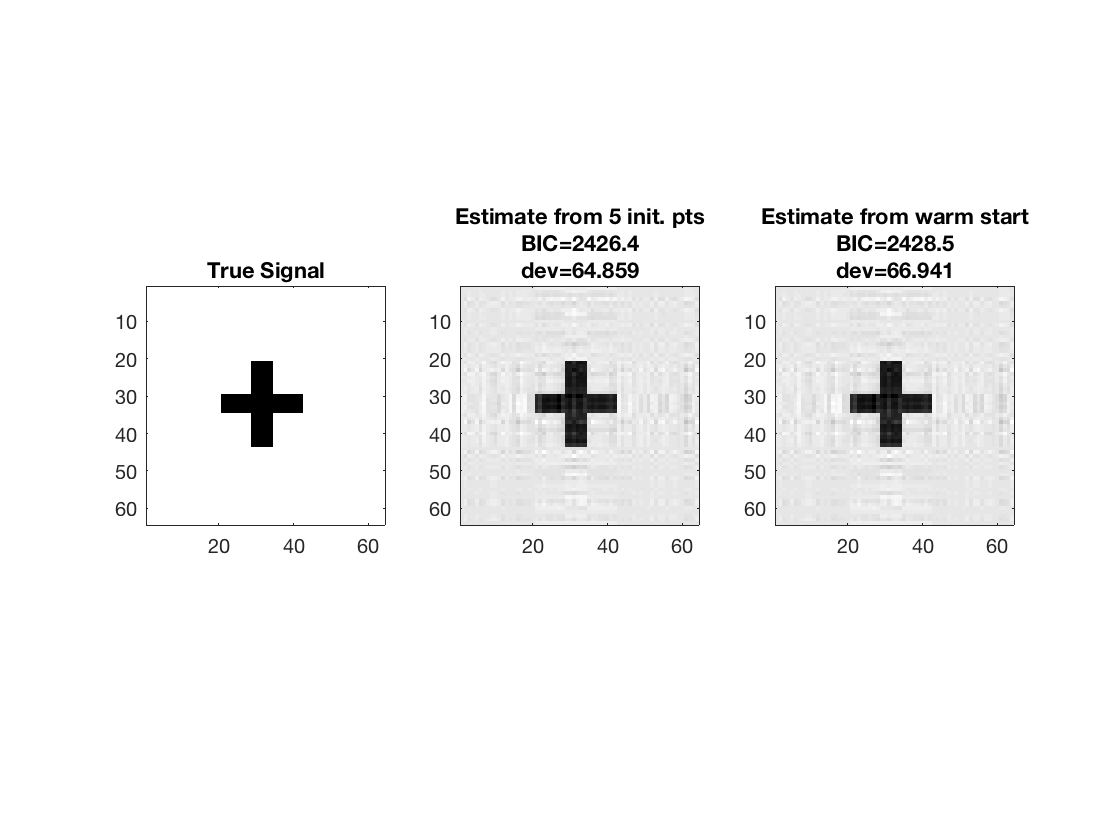
Warm starting from coarsened estimate

% Reduce array covariates to smaller size and fit rank-3 model
tic;
M_small = array_resize(M, [16 16 size(M,3)]);
[~,beta_small] = tucker_reg(X,M_small,y,3,'normal');
disp(size(beta_small));

    16    16

Use coarsened estimate as initial point

[~,beta_ws,glmstats_ws,dev_ws] = tucker_reg(X,M,y,3,'normal', ...
    'B0',array_resize(beta_small,[p1 p2]));
toc;
disp(size(beta_ws));

Elapsed time is 4.380676 seconds.
    64    64

Compare estimate using warm start and previous estimate (5 random initial points)

disp([dev3 dev_ws]);
disp([glmstats3{end}.BIC glmstats_ws{end}.BIC]);

% disp true and recovered signals
figure; hold on;
set(gca,'FontSize',20);

subplot(1,3,1);
imagesc(-b);
colormap(gray);
title('True Signal');
axis equal;
axis tight;

subplot(1,3,2);
imagesc(-double(beta_rk3));
colormap(gray);
title({'Estimate from 5 init. pts'; ...
    ['BIC=',num2str(glmstats3{end}.BIC,5)]; ...
    ['dev=',num2str(dev3,5)]});
axis equal;
axis tight;

subplot(1,3,3);
imagesc(-double(beta_rk3));
colormap(gray);
title({'Estimate from warm start'; ...
    ['BIC=',num2str(glmstats_ws{end}.BIC,5)]; ...
    ['dev=',num2str(dev_ws,5)]});
axis equal;
axis tight;

   64.8592   66.9409

   1.0e+03 *

    2.4264    2.4285

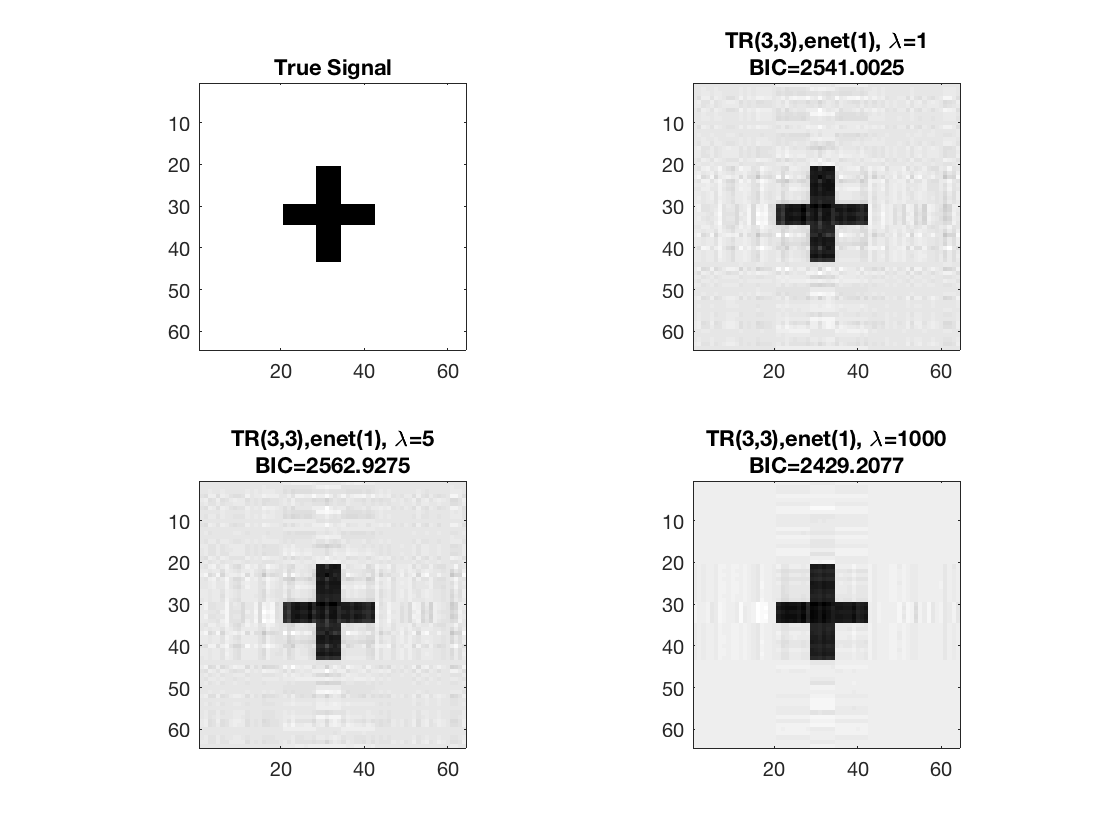
Sparse Tucker linear regression, 2D covariates

Set lasso penalty and tuning parameter values

pentype = 'enet';
penparam = 1;
lambda = [1,5,1000];

Estimate using Tucker sparse linear regression - lambda 1 Warm start from rank 3 estimate

tic;
disp(['lambda=', num2str(lambda(1))]);
[~,beta_rk1,~,glmstat_rk1] = tucker_sparsereg(X,M,y,3,'normal',...
    lambda(1),pentype,penparam,'B0',beta_rk3);
toc;

lambda=1
Elapsed time is 0.885159 seconds.

Estimate using Tucker sparse linear regression - lambda 2 Warm start from rank 3 estimate

tic;
disp(['lambda=', num2str(lambda(2))]);
[~,beta_rk2,~,glmstat_rk2] = tucker_sparsereg(X,M,y,3,'normal',...
    lambda(2),pentype,penparam,'B0',beta_rk3);
toc;

lambda=5
Elapsed time is 0.790504 seconds.

Estimate using Tucker sparse linear regression - lambda 3

tic;
disp(['lambda=', num2str(lambda(3))]);
[~,beta_rk3,~,glmstat_rk3] = tucker_sparsereg(X,M,y,3,'normal',...
    lambda(3),pentype,penparam,'B0',beta_rk3);
toc;

lambda=1000
Elapsed time is 0.312698 seconds.

disp true and recovered signals

figure; hold on;
set(gca,'FontSize',20);

subplot(2,2,1);
imagesc(-b);
colormap(gray);
title('True Signal');
axis equal;
axis tight;

subplot(2,2,2);
imagesc(-double(beta_rk1));
colormap(gray);
title({['TR(3,3),' pentype '(' num2str(penparam), '), \lambda=', ...
    num2str(lambda(1))];...
    ['BIC=', num2str(glmstat_rk1{end}.BIC)]});
axis equal;
axis tight;

subplot(2,2,3);
imagesc(-double(beta_rk2));
colormap(gray);
title({['TR(3,3),' pentype '(' num2str(penparam), '), \lambda=', ...
    num2str(lambda(2))];...
    ['BIC=', num2str(glmstat_rk2{end}.BIC)]});
axis equal;
axis tight;

subplot(2,2,4);
imagesc(-double(beta_rk3));
colormap(gray);
title({['TR(3,3),' pentype '(' num2str(penparam), '), \lambda=', ...
    num2str(lambda(3))];...
    ['BIC=', num2str(glmstat_rk3{end}.BIC)]});
axis equal;
axis tight;

Tucker logistic regression, 2D covariates

clear;
% reset random seed
s = RandStream('mt19937ar','Seed',2);
RandStream.setGlobalStream(s);

true coefficients for regular (non-narray) covariates

p0 = 5;
b0 = ones(p0,1);

2D true signal: 64-by-64 cross

shape = imread('cross.gif');
shape = array_resize(shape,[32,32]); % 32-by-32
b = zeros(2*size(shape));
b((size(b,1)/4):(size(b,1)/4)+size(shape,1)-1, ...
    (size(b,2)/4):(size(b,2)/4)+size(shape,2)-1) = shape;
[p1,p2] = size(b);
disp(size(b));

    64    64

Simulate covariates

n = 1000;    % sample size
X = randn(n,p0);   % n-by-p regular design matrix
M = tensor(randn(p1,p2,n));  % p1-by-p2-by-n matrix variates
disp(size(M));

          64          64        1000

Simulate binary responses from the systematic components

mu = X*b0 + double(ttt(tensor(b), M, 1:2));
y = binornd(1, 1./(1+exp(-mu)));

Estimate using Tucker logistic regression - rank (1 1)

tic;
disp('rank (1 1)');
[beta0_rk1,beta_rk1,glmstats1,dev1] = tucker_reg(X,M,y,[1 1],'binomial');
toc;

rank (1 1)
Elapsed time is 1.596931 seconds.

Estimate using Tucker logistic regression - rank (1 2)

tic;
disp('rank (1 2)');
[~,beta_rk12,glmstats12] = tucker_reg(X,M,y,[1 2],'binomial');
toc;

rank (1 2)
Elapsed time is 2.121412 seconds.

Estimate using Tucker logistic regression - rank (2 2)

tic;
% a rough estimate from reduced sized data
M_reduce = array_resize(M, [16 16 size(M,3)]);
[~,beta_rk2] = tucker_reg(X,M_reduce,y,[2 2],'binomial');
beta_rk2 = array_resize(beta_rk2, [64 64]);
% warm start from coarsened estimate
disp('rank (2 2)');
[~,beta_rk2,glmstats2] = tucker_reg(X,M,y,[2 2],'binomial','B0',beta_rk2);
toc;

rank (2 2)
Elapsed time is 2.681551 seconds.

Estimate using Tucker logistic regression - rank (2 3)

tic;
disp('rank (2 3)');
% a rough estimate from reduced sized data
[~,beta_rk23] = tucker_reg(X,M_reduce,y,[2 3],'binomial');
beta_rk23 = array_resize(beta_rk23, [64 64]);
% warm start from coarsened estimate
[~,beta_rk23,glmstats23] = tucker_reg(X,M,y,[2 3],'binomial','B0',beta_rk23);
toc;

rank (2 3)
Elapsed time is 3.573067 seconds.

Estimate using Tucker logistic regression - rank (3 3)

tic;
disp('rank (3 3)');
% a rough estimate from reduced sized data
[~,beta_rk3] = tucker_reg(X,M_reduce,y,[3 3],'binomial');
beta_rk3 = array_resize(beta_rk3, [64 64]);
% warm start from coarsened estimate
[~,beta_rk3,glmstats3] = tucker_reg(X,M,y,[3 3],'binomial','B0',beta_rk3);
toc;

rank (3 3)
Elapsed time is 8.022493 seconds.

disp true and recovered signals

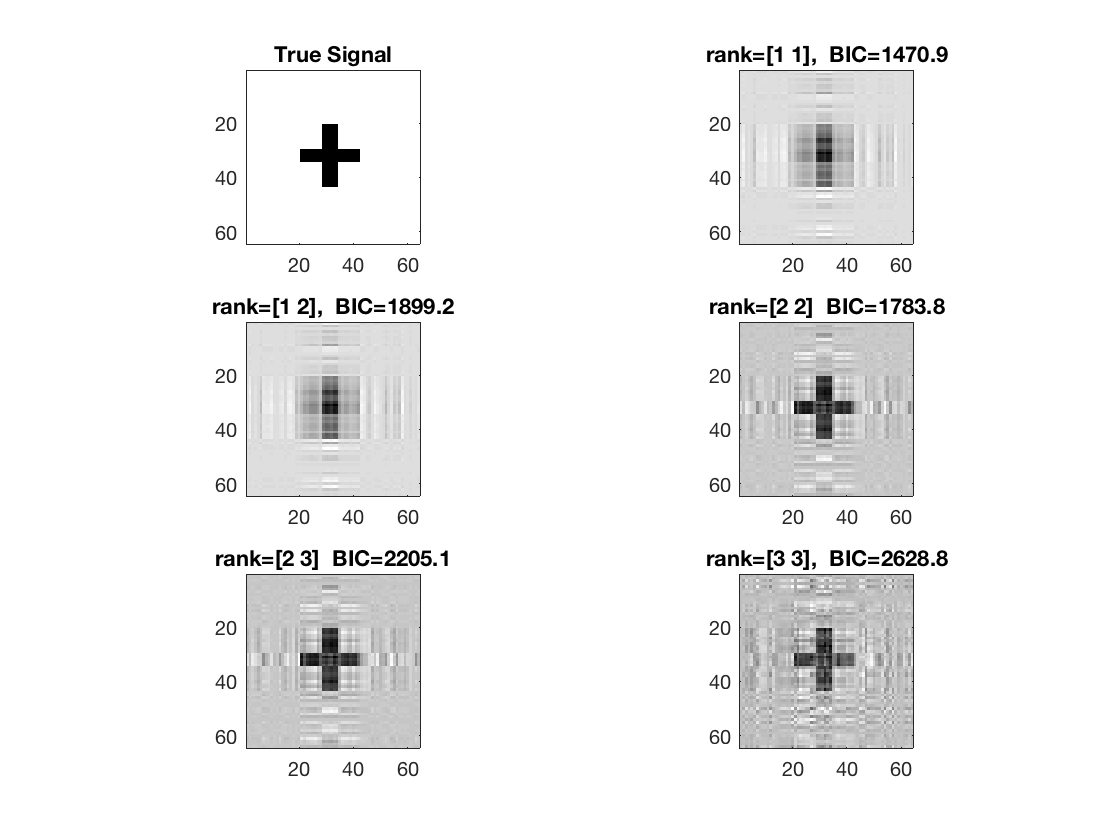
figure; hold on;
set(gca,'FontSize',20);

subplot(3,2,1);
imagesc(-b);
colormap(gray);
title('True Signal');
axis equal;
axis tight;

subplot(3,2,2);
imagesc(-double(beta_rk1));
colormap(gray);
title({['rank=[1 1], ', ' BIC=',num2str(glmstats1{end}.BIC,5)]});
axis equal;
axis tight;

subplot(3,2,3);
imagesc(-double(beta_rk12));
colormap(gray);
title({['rank=[1 2], ', ' BIC=',num2str(glmstats12{end}.BIC,5)]});
axis equal;
axis tight;

subplot(3,2,4);
imagesc(-double(beta_rk2));
colormap(gray);
title({['rank=[2 2] ', ' BIC=',num2str(glmstats2{end}.BIC,5)]});
axis equal;
axis tight;

subplot(3,2,5);
imagesc(-double(beta_rk23));
colormap(gray);
title({['rank=[2 3] ', ' BIC=',num2str(glmstats23{end}.BIC,5)]});
axis equal;
axis tight;

subplot(3,2,6);
imagesc(-double(beta_rk3));
colormap(gray);
title({['rank=[3 3], ', ' BIC=',num2str(glmstats3{end}.BIC,5)]});
axis equal;
axis tight;

Sparse Tucker logistic regression, 2D covariates

Set lasso penalty and tuning parameter values

pentype = 'enet';
penparam = 1;
lambda = [1,10,100];

Estimate using Tucker sparse logistic regression - lambda 1 Warm start from rank 3 estimate

tic;
disp(['lambda=', num2str(lambda(1))]);
[~,beta_rk1,~,glmstat_rk1] = tucker_sparsereg(X,M,y,3,'binomial',...
    lambda(1),pentype,penparam,'B0',beta_rk3);
toc;

lambda=1
Elapsed time is 1.461679 seconds.

Estimate using Tucker sparse logistic regression - lambda 2 Warm start from rank 3 estimate

tic;
disp(['lambda=', num2str(lambda(2))]);
[~,beta_rk2,~,glmstat_rk2] = tucker_sparsereg(X,M,y,3,'binomial',...
    lambda(2),pentype,penparam,'B0',beta_rk3);
toc;

lambda=10
Elapsed time is 4.024404 seconds.

Estimate using Tucker sparse logistic regression - lambda 3 Warm start from rank 3 estimate

tic;
disp(['lambda=', num2str(lambda(3))]);
[~,beta_rk3,~,glmstat_rk3] = tucker_sparsereg(X,M,y,3,'binomial',...
    lambda(3),pentype,penparam,'B0',beta_rk3);
toc;

lambda=100
Elapsed time is 1.478872 seconds.

disp true and recovered signals

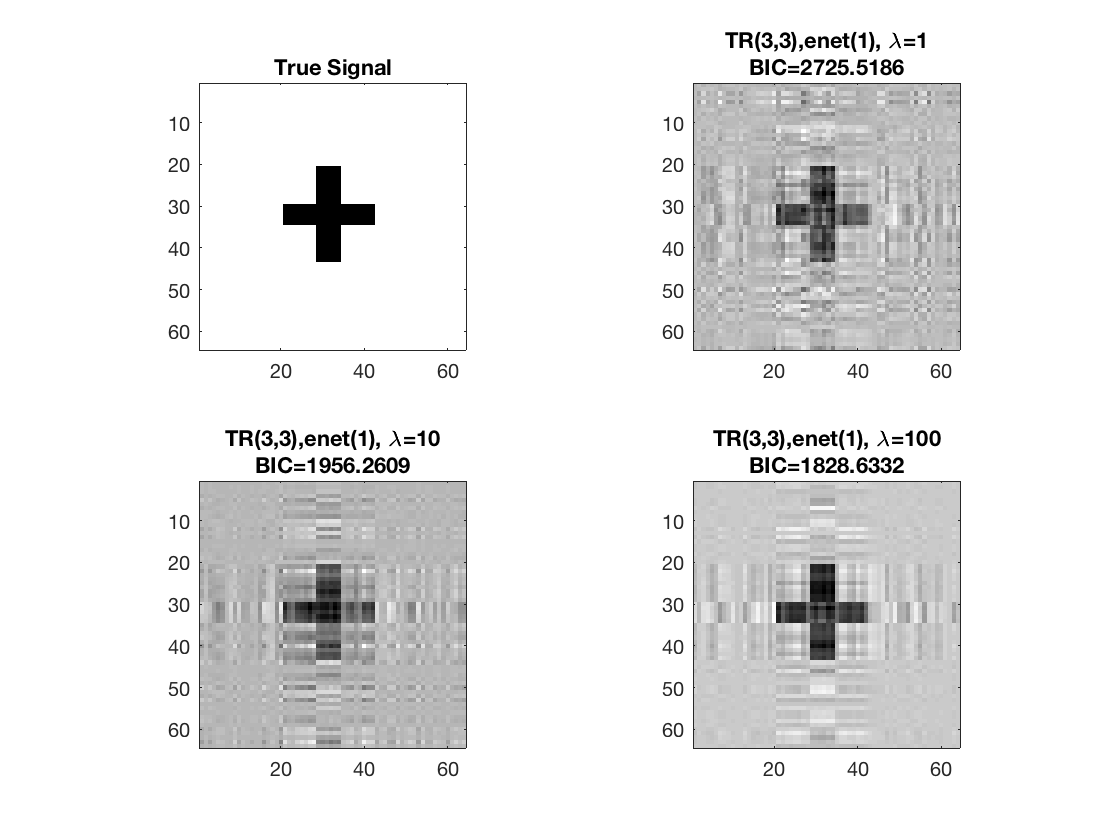
figure; hold on;
set(gca,'FontSize',20);

subplot(2,2,1);
imagesc(-b);
colormap(gray);
title('True Signal');
axis equal;
axis tight;

subplot(2,2,2);
imagesc(-double(beta_rk1));
colormap(gray);
title({['TR(3,3),' pentype '(' num2str(penparam), '), \lambda=', ...
    num2str(lambda(1))];...
    ['BIC=', num2str(glmstat_rk1{end}.BIC)]});
axis equal;
axis tight;

subplot(2,2,3);
imagesc(-double(beta_rk2));
colormap(gray);
title({['TR(3,3),' pentype '(' num2str(penparam), '), \lambda=', ...
    num2str(lambda(2))];...
    ['BIC=', num2str(glmstat_rk2{end}.BIC)]});
axis equal;
axis tight;

subplot(2,2,4);
imagesc(-double(beta_rk3));
colormap(gray);
title({['TR(3,3),' pentype '(' num2str(penparam), '), \lambda=', ...
    num2str(lambda(3))];...
    ['BIC=', num2str(glmstat_rk3{end}.BIC)]});
axis equal;
axis tight;

Tucker linear regression, 3D covariates

clear;
% reset random seed
s = RandStream('mt19937ar','Seed',2);
RandStream.setGlobalStream(s);

True coefficients for regular (non-array) covariates

p0 = 5;
b0 = ones(p0,1);

True 3D signal: 25-by-25-by-25 "two-cube"

b = zeros(25,25,25);
b(6:10,6:10,6:10) = 1;
b(18:22,18:22,8:22) = 1;
[p1, p2, p3] = size(b);
disp(size(b));

    25    25    25

Simulate covariates

n = 500;    % sample size
X = randn(n,p0);   % n-by-p regular design matrix
M = tensor(randn(p1,p2,p3,n));  % p1-by-p2-by-p3 3D variates
% the systematic part
mu = X*b0 + double(ttt(M,tensor(b),1:3));
% simulate responses
sigma = 1;  % noise level
y = mu + sigma*randn(n,1);

Estimate by Tucker linear regression - rank (1 1 1)

tic;
disp('rank (1 1 1)');
[~,beta_rk1,glmstats1] = tucker_reg(X,M,y,[1 1 1],'normal');
toc;

rank (1 1 1)
Elapsed time is 2.741409 seconds.

Estimate by Tucker linear regression - rank (1 2 2)

tic;
disp('rank (1 2 2)');
[~,beta_rk122,glmstats122] = tucker_reg(X,M,y,[1 2 2],'normal');
toc;

rank (1 2 2)
Elapsed time is 5.222631 seconds.

Estimate by Tucker linear regression - rank (2 2 2)

tic;
disp('rank (2 2 2)');
% a rough estimate from reduced sized data
M_reduce = array_resize(M, [10 10 10 size(M,4)]);
[~,beta_rk2] = tucker_reg(X,M_reduce,y,2,'normal');
beta_rk2 = array_resize(beta_rk2, [p1 p2 p3]);
% warm start from coarsened estimate
[~,beta_rk2,glmstats2] = tucker_reg(X,M,y,[2 2 2],'normal','B0',beta_rk2);
toc;

rank (2 2 2)
Elapsed time is 2.998746 seconds.

Estimate by Tucker linear regression - rank (2 3 3)

tic;
disp('rank (2 3 3)');
% a rough estimate from reduced sized data
M_reduce = array_resize(M, [10 10 10 size(M,4)]);
[~,beta_rk233] = tucker_reg(X,M_reduce,y,[2 3 3],'normal');
beta_rk233 = array_resize(beta_rk233, [p1 p2 p3]);
% warm start from coarsened estimate
[~,beta_rk233,glmstats233] = tucker_reg(X,M,y,[2 3 3],'normal','B0',beta_rk233);
toc;

rank (2 3 3)
Elapsed time is 7.274027 seconds.

Estimate by Tucker linear regression - rank (3 3 3)

tic;
disp('rank (3 3 3)');
% a rough estimate from reduced sized data
M_reduce = array_resize(M, [10 10 10 size(M,4)]);
[~,beta_rk3] = tucker_reg(X,M_reduce,y,3,'normal');
beta_rk3 = array_resize(beta_rk3, [p1 p2 p3]);
% warm start from coarsened estimate
[~,beta_rk3,glmstats3] = tucker_reg(X,M,y,[3 3 3],'normal','B0',beta_rk3);
toc;

rank (3 3 3)
Elapsed time is 6.293258 seconds.

disp true and recovered signals

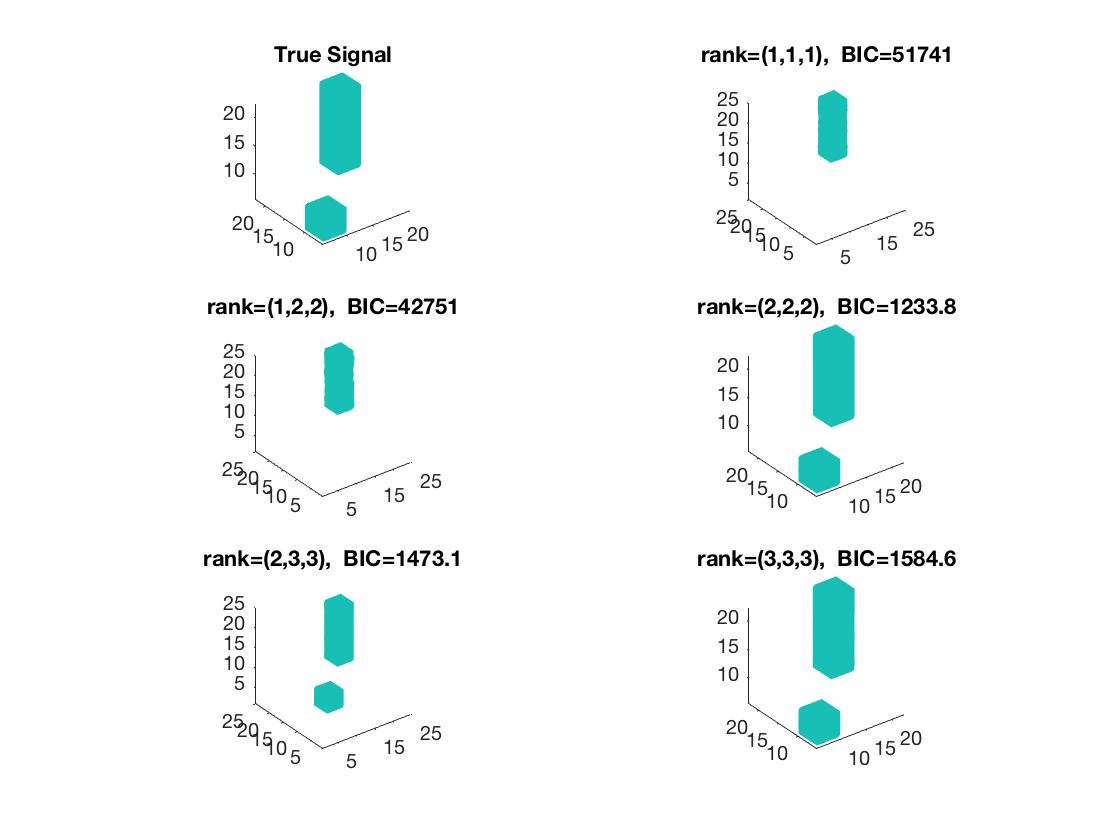
figure; hold on;
set(gca,'FontSize',20);

subplot(3,2,1);
view(3);
isosurface(b,.5);
xlim([1 p1]);
ylim([1 p2]);
zlim([1 p3]);
title('True Signal');
axis equal;

subplot(3,2,2);
isosurface(double(beta_rk1),0.5);
view(3);
xlim([1 p1]);
ylim([1 p2]);
zlim([1 p3]);
title({['rank=(1,1,1), ', ' BIC=', num2str(glmstats1{end}.BIC,5)]});
daspect(daspect);

subplot(3,2,3);
isosurface(double(beta_rk122),0.5);
view(3);
xlim([1 p1]);
ylim([1 p2]);
zlim([1 p3]);
title({['rank=(1,2,2), ', ' BIC=', num2str(glmstats122{end}.BIC,5)]});
daspect(daspect);

subplot(3,2,4);
view(3);
isosurface(double(beta_rk2),0.5);
xlim([1 p1]);
ylim([1 p2]);
zlim([1 p3]);
title({['rank=(2,2,2), ', ' BIC=', num2str(glmstats2{end}.BIC,5)]});
axis equal;

subplot(3,2,5);
isosurface(double(beta_rk233),0.5);
view(3);
xlim([1 p1]);
ylim([1 p2]);
zlim([1 p3]);
title({['rank=(2,3,3), ', ' BIC=', num2str(glmstats233{end}.BIC,5)]});
daspect(daspect);


subplot(3,2,6);
view(3);
isosurface(double(beta_rk3),0.5);
xlim([1 p1]);
ylim([1 p2]);
zlim([1 p3]);
title({['rank=(3,3,3), ', ' BIC=', num2str(glmstats3{end}.BIC,5)]});
axis equal;

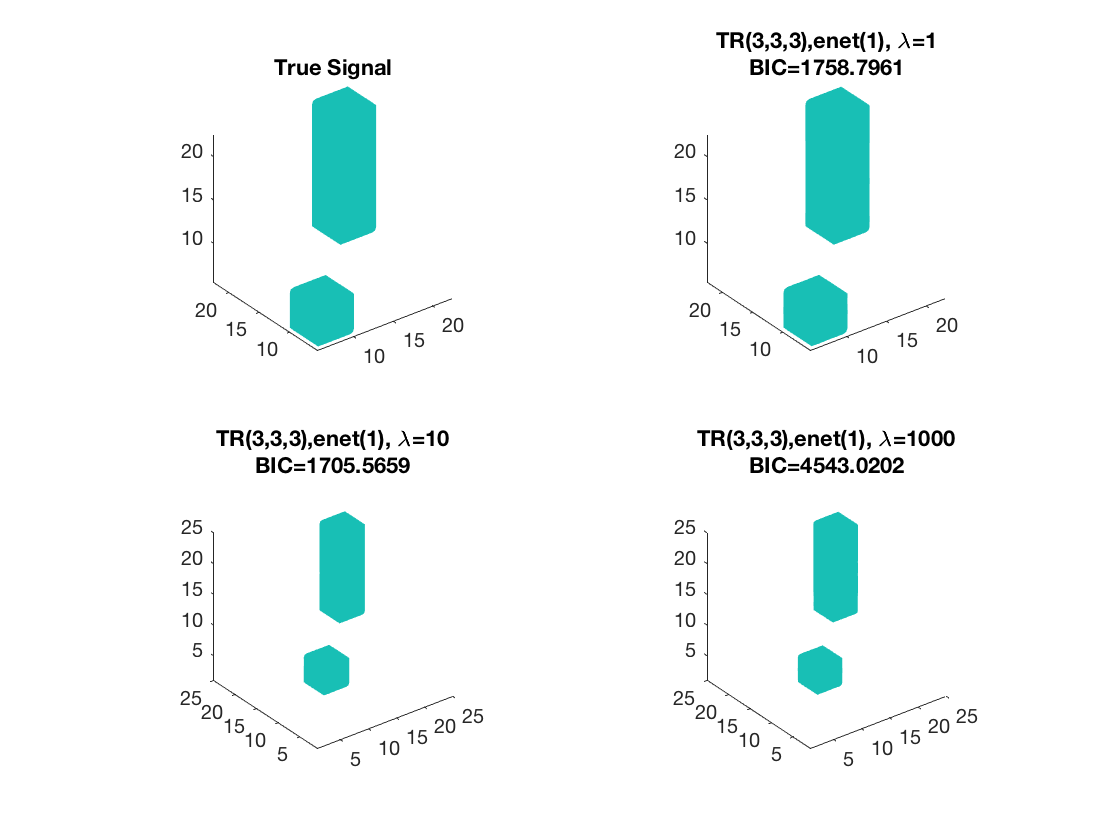
Sparse Tucker linear regression, 3D covaraites,

Set lasso penalty and tuning parameter values

pentype = 'enet';
penparam = 1;
lambda = [1,10,1000];

Estimate using Tucker sparse linear regression - lambda 1 Warm start from rank 3 estimate

tic;
disp(['lambda=', num2str(lambda(1))]);
[~,beta_rk1,~,glmstat_rk1] = tucker_sparsereg(X,M,y,3,'normal',...
    lambda(1),pentype,penparam,'B0',beta_rk3);
toc;

lambda=1
Elapsed time is 0.592070 seconds.

Estimate using Tucker sparse linear regression - lambda 2 Warm start from rank 3 estimate

tic;
disp(['lambda=', num2str(lambda(2))]);
[~,beta_rk2,~,glmstat_rk2] = tucker_sparsereg(X,M,y,3,'normal',...
    lambda(2),pentype,penparam,'B0',beta_rk3);
toc;

lambda=10
Elapsed time is 1.423486 seconds.

Estimate using Tucker sparse linear regression - lambda 3 Warm start from rank 3 estimate

tic;
disp(['lambda=', num2str(lambda(3))]);
[~,beta_rk3,~,glmstat_rk3] = tucker_sparsereg(X,M,y,3,'normal',...
    lambda(3),pentype,penparam,'B0',beta_rk3);
toc;

lambda=1000
Elapsed time is 1.087429 seconds.

disp true and recovered signals

figure; hold on;
set(gca,'FontSize',20);

subplot(2,2,1);
view(3);
isosurface(b,.5);
xlim([1 p1]);
ylim([1 p2]);
zlim([1 p3]);
title('True Signal');
axis equal;

subplot(2,2,2);
isosurface(double(beta_rk1),0.5);
view(3);
xlim([1 p1]);
ylim([1 p2]);
zlim([1 p3]);
daspect(daspect);
title({['TR(3,3,3),' pentype '(' num2str(penparam), '), \lambda=', ...
    num2str(lambda(1))];...
    ['BIC=', num2str(glmstat_rk1{end}.BIC)]});
axis equal;

subplot(2,2,3);
view(3);
isosurface(double(beta_rk2),0.5);
xlim([1 p1]);
ylim([1 p2]);
zlim([1 p3]);
title({['TR(3,3,3),' pentype '(' num2str(penparam), '), \lambda=', ...
    num2str(lambda(2))];...
    ['BIC=', num2str(glmstat_rk2{end}.BIC)]});
daspect(daspect);

subplot(2,2,4);
view(3);
isosurface(double(beta_rk3),0.5);
xlim([1 p1]);
ylim([1 p2]);
zlim([1 p3]);
title({['TR(3,3,3),' pentype '(' num2str(penparam), '), \lambda=', ...
    num2str(lambda(3))];...
    ['BIC=', num2str(glmstat_rk3{end}.BIC)]});
daspect(daspect);

Published with MATLAB® R2017a