Introduction to ...

Acknowledgement

Some slides are taken from Josh Day's presentations:

Types of computer languages

  • Compiled languages: C/C++, Fortran, ...

    • Directly compiled to machine code that is executed by CPU
    • Pros: fast, memory efficient
    • Cons: longer development time, hard to debug

  • Interpreted language: R, Matlab, SAS IML, JavaScript, BASIC, ...

    • Interpreted by interpreter
    • Pros: fast prototyping
    • Cons: excruciatingly slow for loops

  • Mixed (dynamic) languages: Julia, Python, JAVA, Matlab (JIT), R (compiler package), ...

    • Dynamic is versus to the static compiled languages
    • Pros and cons: between the compiled and interpreted languages

  • Script languages: Linux shell scripts, Perl, ...

    • Extremely useful for some data preprocessing and manipulation
    • E.g., massage the Yelp data before analysis

  • Database languages: SQL, Hadoop.
    • Data analysis never happens if we do not know how to retrieve data from databases

Messages

  • To be versatile in the big data era, master at least one language in each category.

  • To improve efficiency of interpreted languages such as R or Matlab, conventional wisdom is to avoid loops as much as possible. Aka, vectorize code

    The only loop you are allowed to have is that for an iterative algorithm.

  • For some tasks where looping is necessary, consider coding in C or Fortran. It is "convenient" to incorporate compiled code into R or Matlab. But do this only after profiling.
    Success stories: glmnet packages in R is coded in Fortran.

  • Modern languages such as Julia tries to solve the two language problem. That is to achieve efficiency without vectorizing code.

What's Julia?

Julia is a high-level, high-performance dynamic programming language for technical computing, with syntax that is familiar to users of other technical computing environments

  • Started in 2009. First public release in 2012.

    • Creators: Jeff Bezanson, Alan Edelman, Stefan Karpinski, Viral Shah
    • Current release v0.5.1
    • v1.0 is staged to release in 2017

  • Aims to solve the notorious "two language problem":

    • Prototype code goes into high-level languages like R/Python, production code goes into low-level language like C/C++

  • Write high-level, abstract code that closely resembles mathematical formulas

    • yet produces fast, low-level machine code that has traditionally only been generated by static languages.

  • Julia is more than just "Fast R" or "Fast Matlab"

    • Performance comes from features that work well together.
    • You can't just take the magic dust that makes Julia fast and sprinkle it on [language of choice]

R is great, but...

  • It's not meant for high performance computing

  • Deficiencies in the core language

    • Some fixed with packages (devtools, roxygen2, Matrix)
    • Others harder to fix (R uses an old version of BLAS)
    • Some impossible to fix (clunky syntax, poor design choices)

  • Only 6 active developers left (out of 20 R-Core members)

  • Doug Bates (member of R-Core, Matrix and lme4)

    • Getting Doug on board was a big win for statistics with Julia, as he brought a lot of knowledge about the history of R development and design choices

    • https://github.com/dmbates/MixedModels.jl

      As some of you may know, I have had a (rather late) mid-life crisis and run off with another language called Julia.

      -- Doug Bates (on the `knitr` Google Group)

Language features of R, Matlab and Julia

Features R Matlab Julia
Open source 👍 👎 👍
IDE RStudio 👍 👍 👍 👍 👍 Atom+Juno 👎
Dynamic document RMarkdown 👍 👍 👍 👍 👍 IJulia 👍 👍
Multi-threading parallel 👎 👍 👍 👍 see docs
JIT compiler 👎 👍 👍 👍 👍 👍
Call C/Fortran wrapper, Rcpp wrapper no glue code needed
Call shared library wrapper wrapper no glue code needed
Type system 👎 👍 👍 👍 👍 👍
Pass by reference 👎 👎 👍 👍 👍
Linear algebra 👎 MKL, Arpack OpenBLAS, eigpack
Distributed computing 👎 👍 👍 👍 👍
Sparse linear algebra Matrix package 👎 👍 👍 👍 👍 👍 👍
Documentation 👎 👍 👍 👍 👍 👍
Profiler 👎 👍 👍 👍 👍 👍 👍

Benchmark

Test R 3.3.2 Matlab R2017a Julia 0.5.1
Matrix creation, trans., deform. (2500 x 2500) 0.70 0.13 0.22
Power of matrix (2500 x 2500, A.^1000) 0.17 0.10 0.11
Quick sort ($n = 7 \times 10^6$) 0.69 0.30 0.62
Cross product (2800 x 2800, $A^TA$) 13.49 0.18 0.21
LS solution ($n = p = 2000$) 6.42 0.07 0.07
FFT ($n = 2,400,000$) 0.25 0.03 0.16
Eigen-values ($600 \times 600$) 0.71 0.22 0.51
Determinant ($2500 \times 2500$) 3.49 0.19 0.14
Cholesky ($3000 \times 3000$) 5.03 0.08 0.16
Matrix inverse ($1600 \times 1600$) 2.83 0.11 0.18
Fibonacci (vector calculation) 0.22 0.16 0.58
Hilbert (matrix calculation) 0.21 0.07 0.06
GCD (recursion) 0.33 0.09 0.13
Toeplitz matrix (loops) 0.28 0.0012 0.0007
Escoufiers (mixed) 0.33 0.15 0.14

Machine specs: Intel i7 @ 2.9GHz (4 physical cores, 8 threads), 16G RAM, Mac OS 10.12.3.

Gibbs sampler example by Doug Bates

  • An example from Dr. Doug Bates's slides Julia for R Programmers.

  • The task is to create a Gibbs sampler for the density
    $$ f(x, y) = k x^2 exp(- x y^2 - y^2 + 2y - 4x), x > 0 $$ using the conditional distributions $$ \begin{eqnarray*} X | Y &\sim& \Gamma \left( 3, \frac{1}{y^2 + 4} \right) \\ Y | X &\sim& N \left(\frac{1}{1+x}, \frac{1}{2(1+x)} \right). \end{eqnarray*} $$

  • This is a Julia function for the simple Gibbs sampler:

In [1]:
using Distributions

function jgibbs(N, thin)
    mat = zeros(N, 2)
    x = y = 0.0
    for i in 1:N
        for j in 1:thin
            x = rand(Gamma(3.0, 1.0 / (y * y + 4.0)))
            y = rand(Normal(1.0 / (x + 1.0), 1.0 / sqrt(2.0(x + 1.0))))
        end
        mat[i, 1] = x
        mat[i, 2] = y
    end
    mat
end
Out[1]:
jgibbs (generic function with 1 method)

Generate a bivariate sample of size 10,000 with a thinning of 500. How long does it take?

In [2]:
jgibbs(100, 5); # warm-up
@elapsed jgibbs(10000, 500)
Out[2]:
0.297332393
  • R solution. The RCall.jl package allows us to execute R code without leaving the Julia environment. We first define an R function Rgibbs().
In [3]:
using RCall

R"""
library(Matrix)
Rgibbs <- function(N, thin) {
  mat <- matrix(0, nrow=N, ncol=2)
  x <- y <- 0
  for (i in 1:N) {
    for (j in 1:thin) {
      x <- rgamma(1, 3, y * y + 4) # 3rd arg is rate
      y <- rnorm(1, 1 / (x + 1), 1 / sqrt(2 * (x + 1)))
    }
    mat[i,] <- c(x, y)
  }
  mat
}
"""
Out[3]:
RCall.RObject{RCall.ClosSxp}
function (N, thin) 
{
    mat <- matrix(0, nrow = N, ncol = 2)
    x <- y <- 0
    for (i in 1:N) {
        for (j in 1:thin) {
            x <- rgamma(1, 3, y * y + 4)
            y <- rnorm(1, 1/(x + 1), 1/sqrt(2 * (x + 1)))
        }
        mat[i, ] <- c(x, y)
    }
    mat
}

and then generate the same number of samples

In [4]:
# warm up 
R"""
Rgibbs(100, 5)
"""
# benchmark
@elapsed R"""
system.time(Rgibbs(10000, 500))
"""
Out[4]:
26.406300151

We see 80-100 fold speed up of Julia over R on this example, without extra coding effort!

Some resources for learning Julia

  1. Read a cheat sheet by Ian Hellstrom, The Fast Track to Julia.
  2. Browse the Julia documentation.
  3. The tutorials Hands-on Julia by Dr. David P. Sanders are excellent.
  4. For Matlab users, read Noteworthy Differences From Matlab.
    For R users, read Noteworthy Differences From R.
    For Python users, read Noteworthy Differences From Python.
  5. The Learning page on Julia's website has pointers to many other learning resources.
  6. Tons of slides/notebooks at http://ucidatascienceinitiative.github.io/IntroToJulia/.

Julia REPL (Read-Evaluation-Print-Loop)

The Julia REPL has four main modes.

  1. Default mode is the Julian prompt julia>. Type backspace in other modes to enter default mode.

  2. Help mode help?>. Type ? to enter help mode. ?search_term does a fuzzy search for search_term.

  3. Shell mode shell>. Type ; to enter shell mode.

  4. Search mode (reverse-i-search). Press ctrl+R to enter search model.

With RCall.jl package installed, we can enter the R mode by typing $ at Julia REPL.

Which IDE?

Julia package system

  • Each Julia package is a git repository.

  • Each Julia package name ends with .jl.
    Google search with PackageName.jl usually leads to the package on github.com easily.

  • For example, the package called Distributions.jl is added with

    Pkg.add("Distributions")   # no .jl

    and "removed" (although not completely deleted) with

    Pkg.rm("Distributions")

  • The package manager provides a dependency solver that determines which packages are actually required to be installed.

  • The package ecosystem is rapidly maturing; a complete list of registered packages (which are required to have a certain level of testing and documentation) is at http://pkg.julialang.org/.

  • Non-registered packages are added by cloning the relevant git repository. E.g.,

    Pkg.clone("git@github.com:OpenMendel/SnpArrays.jl.git")

  • A package need only be added once, at which point it is downloaded into your local .julia/vx.x directory in your home directory. If you start having problems with packages that seem to be unsolvable, you can try just deleting your .julia directory and reinstalling all your packages.

  • Periodically, you should run Pkg.update() which checks for, downloads and installs updated versions of all the packages you currently have installed.

  • Pkg.status() lists the status of all installed packages.

  • Using functions in package.

    using Distributions

    This pulls all of the exported functions in the module into your local namespace, as you can check using the whos() command. An alternative is

    import Distributions

    Now, the functions from the Distributions package are available only using

    Distributions.<FUNNAME>

    All functions, not only exported functions, are always available like this.

JuliaStats

A collection of many statistical packages in Julia:

StatsBase.jl

  • Provides many common functions in base R that are not in base Julia (sampling, weighted statistics, etc.).

  • Also provides many function names (coef, coeftable, predict, etc.) to help packages avoid name conflicts.

In [5]:
using StatsBase

sample(1:5, 5, replace = false)
Out[5]:
5-element Array{Int64,1}:
 4
 5
 2
 3
 1

DataFrames.jl

  • Similar to data frames in R.

  • Import, export, and massage tabular data.

DataTables.jl

  • For working with tabular data with possibly missing values.
  • A fork of DataFrames.jl.
    • The difference is the Array type used on the backend (DistributedArrays vs. NullableArrays) for handling missing data
In [6]:
using DataTables

iris = readtable(joinpath(Pkg.dir("DataTables"), "test/data/iris.csv"))
head(iris)

WARNING: Method definition describe(AbstractArray) in module DataFrames at /Users/huazhou/.julia/v0.5/DataFrames/src/abstractdataframe/abstractdataframe.jl:407 overwritten in module DataTables at /Users/huazhou/.julia/v0.5/DataTables/src/abstractdatatable/abstractdatatable.jl:381.
WARNING: Method definition describe(Any, AbstractArray{#T<:Number, N<:Any}) in module DataFrames at /Users/huazhou/.julia/v0.5/DataFrames/src/abstractdataframe/abstractdataframe.jl:409 overwritten in module DataTables at /Users/huazhou/.julia/v0.5/DataTables/src/abstractdatatable/abstractdatatable.jl:383.
WARNING: Method definition describe(Any, AbstractArray{#T<:Any, N<:Any}) in module DataFrames at /Users/huazhou/.julia/v0.5/DataFrames/src/abstractdataframe/abstractdataframe.jl:426 overwritten in module DataTables at /Users/huazhou/.julia/v0.5/DataTables/src/abstractdatatable/abstractdatatable.jl:400.
Out[6]:
SepalLengthSepalWidthPetalLengthPetalWidthSpecies
15.13.51.40.2setosa
24.93.01.40.2setosa
34.73.21.30.2setosa
44.63.11.50.2setosa
55.03.61.40.2setosa
65.43.91.70.4setosa

Query.jl

  • Query just about any data source.
In [7]:
using Query

x = @from i in iris begin
    @where i.Species == "setosa" && i.PetalLength > 1.7
    @select i
    @collect DataTable
end

WARNING: Method definition require(Symbol) in module Base at loading.jl:345 overwritten in module Query at /Users/huazhou/.julia/v0.5/Requires/src/require.jl:12.
WARNING: Method definition ==(Base.Nullable{#T<:Any}, Base.Nullable{Union{}}) in module NullableArrays at /Users/huazhou/.julia/v0.5/NullableArrays/src/operators.jl:138 overwritten in module Query at /Users/huazhou/.julia/v0.5/Query/src/operators.jl:8.
WARNING: Method definition ==(Base.Nullable{Union{}}, Base.Nullable{#T<:Any}) in module NullableArrays at /Users/huazhou/.julia/v0.5/NullableArrays/src/operators.jl:137 overwritten in module Query at /Users/huazhou/.julia/v0.5/Query/src/operators.jl:9.
WARNING: Method definition ==(Base.Nullable{#T1<:Any}, Base.Nullable{#T2<:Any}) in module NullableArrays at /Users/huazhou/.julia/v0.5/NullableArrays/src/operators.jl:128 overwritten in module Query at /Users/huazhou/.julia/v0.5/Query/src/operators.jl:77.
Out[7]:
SepalLengthSepalWidthPetalLengthPetalWidthSpecies
14.83.41.90.2setosa
25.13.81.90.4setosa

Calling R from Julia

  • The RCall.jl package allows you to embed R code inside of Julia.

  • There are also PyCall, MATLAB, JavaCall, CxxWrap packages.

In [8]:
using RCall

x = randn(1000)
R"""
hist($x, main="I'm plotting a Julia vector")
"""
Out[8]:
RCall.RObject{RCall.VecSxp}
$breaks
 [1] -3.0 -2.5 -2.0 -1.5 -1.0 -0.5  0.0  0.5  1.0  1.5  2.0  2.5  3.0  3.5

$counts
 [1]   2  19  56  86 151 177 208 155  96  41   8   0   1

$density
 [1] 0.004 0.038 0.112 0.172 0.302 0.354 0.416 0.310 0.192 0.082 0.016 0.000
[13] 0.002

$mids
 [1] -2.75 -2.25 -1.75 -1.25 -0.75 -0.25  0.25  0.75  1.25  1.75  2.25  2.75
[13]  3.25

$xname
[1] "`#JL`$x"

$equidist
[1] TRUE

attr(,"class")
[1] "histogram"
In [9]:
R"""
library(ggplot2)
qplot($x) 
"""

WARNING: RCall.jl: `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
Out[9]:
RCall.RObject{RCall.VecSxp}
In [10]:
x = R"""
rnorm(10)
"""
Out[10]:
RCall.RObject{RCall.RealSxp}
 [1]  2.440957952 -1.673411697 -0.219074727  0.175992286 -0.500274911
 [6]  1.314593635 -0.304737664 -0.271341157 -0.007993153  0.043802623
In [11]:
collect(x)
Out[11]:
10-element Array{Float64,1}:
  2.44096   
 -1.67341   
 -0.219075  
  0.175992  
 -0.500275  
  1.31459   
 -0.304738  
 -0.271341  
 -0.00799315
  0.0438026

Some basic Julia code

In [12]:
y = 1
Out[12]:
1
In [13]:
typeof(y)
Out[13]:
Int64
In [14]:
y = 1.0
Out[14]:
1.0
In [15]:
typeof(y)
Out[15]:
Float64
In [16]:
# Greek letters!  `\pi<tab>`
θ = y + π
Out[16]:
4.141592653589793
In [17]:
# emoji! `\:kissing_cat:<tab>`
😽 = 5.0
Out[17]:
5.0
In [18]:
# vector 0s
x = zeros(5)
Out[18]:
5-element Array{Float64,1}:
 0.0
 0.0
 0.0
 0.0
 0.0
In [19]:
# matrix of 0s
x = zeros(5, 3)
Out[19]:
5×3 Array{Float64,2}:
 0.0  0.0  0.0
 0.0  0.0  0.0
 0.0  0.0  0.0
 0.0  0.0  0.0
 0.0  0.0  0.0
In [20]:
# uniform random numbers
x = rand(5, 3)
Out[20]:
5×3 Array{Float64,2}:
 0.338312   0.00273617  0.0127764
 0.368428   0.90842     0.159506 
 0.50596    0.862716    0.0165604
 0.0182879  0.243639    0.464263 
 0.444819   0.177826    0.616423
In [21]:
# standard normal random numbers
x = randn(5, 3)
Out[21]:
5×3 Array{Float64,2}:
 -0.944219  -0.213555    1.61691 
 -0.267622  -1.89073     0.393222
 -0.825686  -1.00155     1.26219 
  0.659843   0.0421919   1.54711 
  0.760456  -0.144578   -1.76404
In [22]:
# range
1:10
Out[22]:
1:10
In [23]:
typeof(1:10)
Out[23]:
UnitRange{Int64}
In [24]:
x = collect(1:10)
Out[24]:
10-element Array{Int64,1}:
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
In [25]:
x = collect(1.0:10)
Out[25]:
10-element Array{Float64,1}:
  1.0
  2.0
  3.0
  4.0
  5.0
  6.0
  7.0
  8.0
  9.0
 10.0
In [26]:
convert(Vector{Float64}, 1:10)
Out[26]:
10-element Array{Float64,1}:
  1.0
  2.0
  3.0
  4.0
  5.0
  6.0
  7.0
  8.0
  9.0
 10.0

Linear algebra

Basic indexing

In [27]:
# 5 × 5 matrix of random Normal(0, 1)
x = randn(5, 5)
Out[27]:
5×5 Array{Float64,2}:
  0.678793  -0.0892747  -1.66113   0.834813   0.806683
 -0.177505   0.704445    0.727904  0.417831  -0.473584
 -0.589874  -1.85191     0.149531  0.387024  -0.898975
 -0.180895  -0.355375    0.469892  0.530244  -0.73835 
  0.214563   0.423059    0.207146  0.825476  -0.927395
In [28]:
# get first column
x[:, 1]
Out[28]:
5-element Array{Float64,1}:
  0.678793
 -0.177505
 -0.589874
 -0.180895
  0.214563
In [29]:
# get first row
x[1, :]
Out[29]:
5-element Array{Float64,1}:
  0.678793 
 -0.0892747
 -1.66113  
  0.834813 
  0.806683
In [30]:
# getting a subset of a matrix creates a copy, but you can also create "views"
@view x[2:end, 1:(end-2)]
Out[30]:
4×3 SubArray{Float64,2,Array{Float64,2},Tuple{UnitRange{Int64},UnitRange{Int64}},false}:
 -0.177505   0.704445  0.727904
 -0.589874  -1.85191   0.149531
 -0.180895  -0.355375  0.469892
  0.214563   0.423059  0.207146

Support for Sparse Matrices

In [31]:
# 10-by-10 sparse matrix with sparsity 0.1
X = sprandn(10, 10, .1)
Out[31]:
10×10 sparse matrix with 11 Float64 nonzero entries:
	[4 ,  1]  =  -0.984458
	[10,  1]  =  0.976949
	[10,  2]  =  -0.26817
	[8 ,  3]  =  -0.0645886
	[5 ,  4]  =  0.302032
	[4 ,  6]  =  -0.629619
	[2 ,  8]  =  -0.109962
	[5 ,  8]  =  -1.43743
	[10,  8]  =  -0.390174
	[2 ,  9]  =  0.990793
	[6 ,  9]  =  0.526542
In [32]:
# syntax for sparse linear algebra is same
β = ones(10)
X * β
Out[32]:
10-element Array{Float64,1}:
  0.0      
  0.880831 
  0.0      
 -1.61408  
 -1.1354   
  0.526542 
  0.0      
 -0.0645886
  0.0      
  0.318605

Call BLAS/LAPACK functions directly

In [33]:
using BenchmarkTools

y = zeros(1000)
x = ones(1000)
@benchmark BLAS.axpy!(0.5, x, y)  # y = 0.5 * x + y
Out[33]:
BenchmarkTools.Trial: 
  memory estimate:  0 bytes
  allocs estimate:  0
  --------------
  minimum time:     1.216 μs (0.00% GC)
  median time:      1.337 μs (0.00% GC)
  mean time:        1.432 μs (0.00% GC)
  maximum time:     7.065 μs (0.00% GC)
  --------------
  samples:          10000
  evals/sample:     10
  time tolerance:   5.00%
  memory tolerance: 1.00%
In [34]:
@benchmark z = .5 * x + y
Out[34]:
BenchmarkTools.Trial: 
  memory estimate:  15.88 KiB
  allocs estimate:  2
  --------------
  minimum time:     1.186 μs (0.00% GC)
  median time:      2.169 μs (0.00% GC)
  mean time:        4.084 μs (32.58% GC)
  maximum time:     298.158 μs (98.27% GC)
  --------------
  samples:          10000
  evals/sample:     10
  time tolerance:   5.00%
  memory tolerance: 1.00%

Functions

  • Defining functions on one line.
    • ::SomeType is a (optional) type annotation
    • I only want my regression function to work with a Matrix and a Vector
In [35]:
regression(x::Matrix, y::Vector) = x \ y
Out[35]:
regression (generic function with 1 method)
  • Defining functions on multiple lines.
    • Code blocks (for loops, if statements, etc., require an end)
    • Function returns the values in the last line
In [36]:
function regression(x::Matrix{Float64}, y::Vector{Float64})
    x \ y
end
Out[36]:
regression (generic function with 2 methods)
  • Using our regression function
In [37]:
srand(123) # random seed
x = randn(100, 5)
y = randn(100)
@show typeof(x), typeof(y)
regression(x, y)

(typeof(x),typeof(y)) = (Array{Float64,2},Array{Float64,1})
Out[37]:
5-element Array{Float64,1}:
 -0.0761932
  0.0197167
 -0.147183 
  0.0613367
 -0.0844392
  • Which function are we using?
In [38]:
@which regression(x, y)
Out[38]:
regression(x::Array{Float64,2}, y::Array{Float64,1}) at In[36]:2
In [39]:
x2 = randn(Float32, 100, 5)
y2 = randn(Float32, 100)
typeof(x2), typeof(y2)
Out[39]:
(Array{Float32,2},Array{Float32,1})
In [40]:
@which regression(x2, y2)
Out[40]:
regression(x::Array{T<:Any,2}, y::Array{T<:Any,1}) at In[35]:1

  • Some types are parameterized by another type.

    • Matrix{Float64} is a two-dimensional array where each element is a Float64
    • Note: Matrix{T} is an alias for Array{T, 2}
    • Our first definition of regression will accept a Matrix and Vector with any element types.
      The second definition is more restrictive.

  • We have not overwritten the previous definition!

    • We have added a method
    • This is called multiple dispatch
      • Different code is called depending on the types of the arguments
      • The most specific method available is called
In [41]:
methods(regression)
Out[41]:
2 methods for generic function regression:
  • regression(x::Array{Float64,2}, y::Array{Float64,1}) at In[36]:2
  • regression(x::Array{T<:Any,2}, y::Array{T<:Any,1}) at In[35]:1

Type system

  • When thinking about types, think about sets.

  • Everything is a subtype of the abstract type Any.

  • An abstract type defines a set of types

    • Consider types in Julia that are a Number:

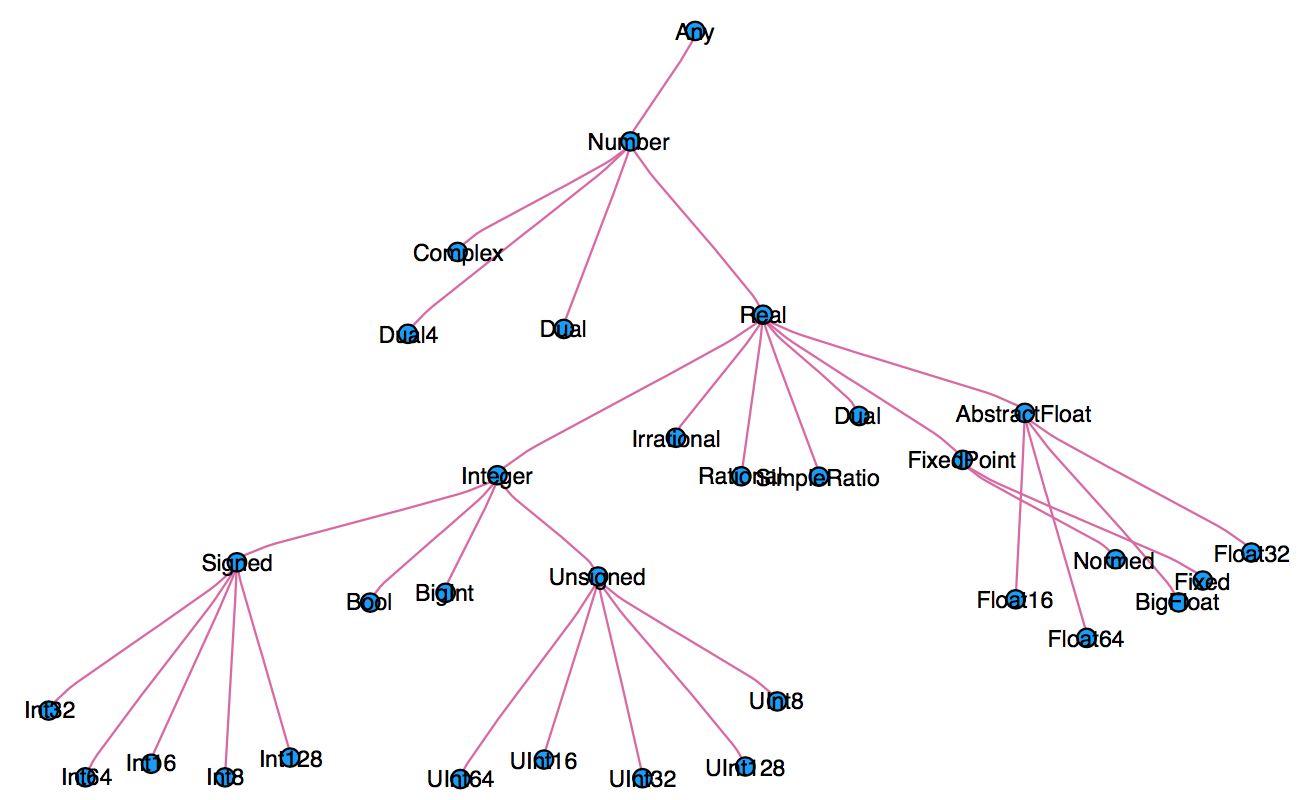
  • You can explore type hierarchy with typeof(), supertype(), and subtypes().
In [42]:
typeof(1.0), typeof(1)
Out[42]:
(Float64,Int64)
In [43]:
supertype(Float64)
Out[43]:
AbstractFloat
In [44]:
subtypes(AbstractFloat)
Out[44]:
4-element Array{Any,1}:
 BigFloat
 Float16 
 Float32 
 Float64
In [45]:
# Is Float64 a subtype of AbstractFloat?
Float64 <: AbstractFloat
Out[45]:
true

  • What properties does a Number have?

    • You can add numbers (+)
    • You can multiply numbers (*)
    • etc.

  • This definition is too broad, since some things can't be added

    g(x) = x + x

  • This definition is too restrictive, since any Number can be added

    g(x::Float64) = x + x

  • This will automatically work on the entire type tree above!

    g(x::Number) = x + x

    This is a lot nicer than

    function g(x)
  if isa(x, Number)
      return x + x
  else
      throw(ArgumentError("x should be a number"))
  end
end

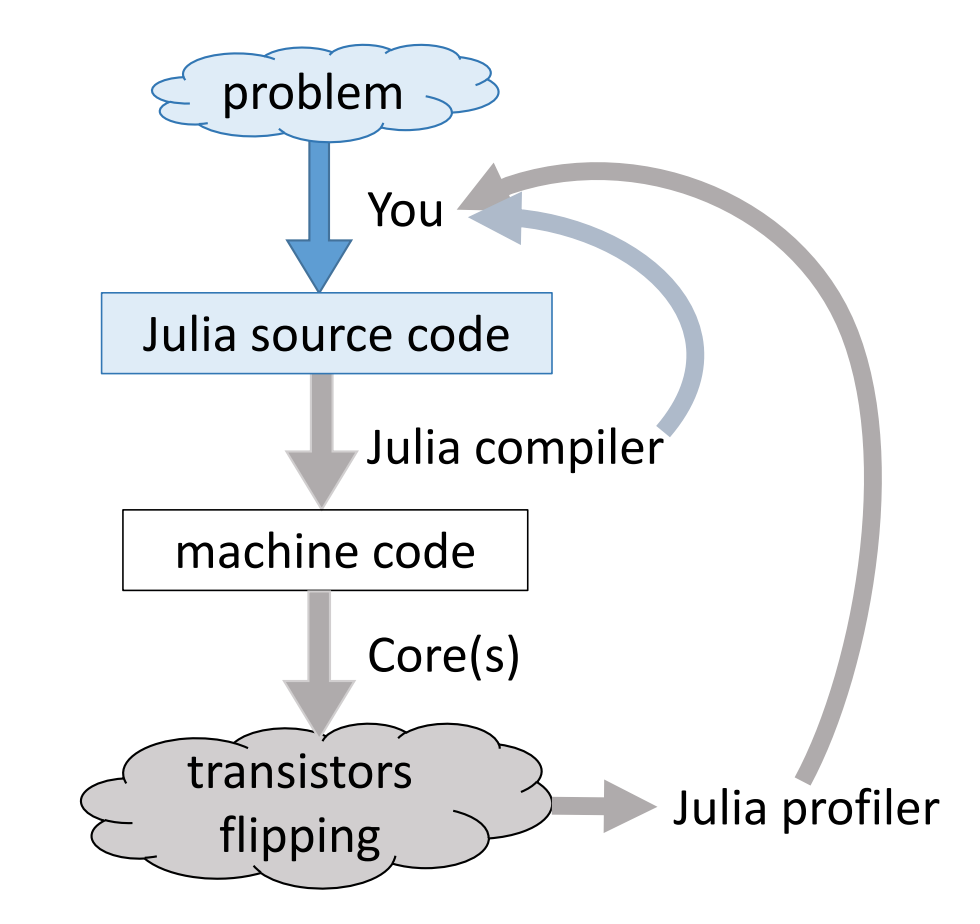
Just-in-time compilation (JIT)

Following figures and some examples are taken from Arch D. Robinson's slides Introduction to Writing High Performance Julia.

Julia toolchain Julia toolchain
In [46]:
x = randn(100)
@time sum(x) # first call invokes compilation
@time sum(x) # second run doesn't need compilation anymore

  0.001187 seconds (14 allocations: 784 bytes)
  0.000002 seconds (5 allocations: 176 bytes)
Out[46]:
-3.557937701148848
  • Julia's efficiency results from its capabilities to infer the types of all variables within a function and then call LLVM to generate optimized machine code at run-time.
In [47]:
g(x) = x + x
Out[47]:
g (generic function with 1 method)

This function will work on any type which has a method for +.

In [48]:
@show g(2)
@show g(2.0);

g(2) = 4
g(2.0) = 4.0

This the abstract syntax tree.

In [49]:
@code_lowered g(2)
Out[49]:
LambdaInfo template for g(x) at In[47]:1
:(begin 
        nothing
        return x + x
    end)

Peek at the compiled code (LLVM bitcode) with @code_llvm

In [50]:
@code_llvm g(2)

define i64 @julia_g_73461(i64) #0 {
top:
  %1 = shl i64 %0, 1
  ret i64 %1
}
In [51]:
@code_llvm g(2.0)

define double @julia_g_73465(double) #0 {
top:
  %1 = fadd double %0, %0
  ret double %1
}

We didn't provide a type annotation. But different code gets called depending on the argument type!

  • In R or Python, g(2) and g(2.0) would use the same code for both.

  • In Julia, g(2) and g(2.0) dispatches to optimized code for Int64 and Float64, respectively.

  • For integer input x, LLVM compiler is smart enough to know x + x is simple shifting x by 1 bit, which is faster than addition.

This is assembly code, which is machin dependent.

In [52]:
@code_native g(2)

	.section	__TEXT,__text,regular,pure_instructions
Filename: In[47]
	pushq	%rbp
	movq	%rsp, %rbp
Source line: 1
	leaq	(%rdi,%rdi), %rax
	popq	%rbp
	retq
	nopw	(%rax,%rax)
In [53]:
@code_native g(2.0)

	.section	__TEXT,__text,regular,pure_instructions
Filename: In[47]
	pushq	%rbp
	movq	%rsp, %rbp
Source line: 1
	addsd	%xmm0, %xmm0
	popq	%rbp
	retq
	nopw	(%rax,%rax)

Profiling Julia code

Julia has several built-in tools for profiling. The @time marco outputs run time and heap allocation.

In [54]:
function tally(x)
    s = 0
    for v in x
        s += v
    end
    s
end

a = rand(10000)
@time tally(a) # warm up: include compile time

  0.010123 seconds (31.56 k allocations: 535.665 KB)
Out[54]:
4997.209569504056
In [55]:
@time tally(a)

  0.000449 seconds (30.00 k allocations: 468.906 KB)
Out[55]:
4997.209569504056

For more robust benchmarking, the BenchmarkTools.jl package is highly recommended.

In [56]:
using BenchmarkTools

@benchmark tally(a)
Out[56]:
BenchmarkTools.Trial: 
  memory estimate:  468.75 KiB
  allocs estimate:  30000
  --------------
  minimum time:     172.875 μs (0.00% GC)
  median time:      197.702 μs (0.00% GC)
  mean time:        227.048 μs (10.48% GC)
  maximum time:     2.302 ms (81.41% GC)
  --------------
  samples:          10000
  evals/sample:     1
  time tolerance:   5.00%
  memory tolerance: 1.00%

We see the heap allocation (average 10.73% GC) is suspiciously high.

The Profile module gives line by line profile results.

In [57]:
a = rand(10000000)
Profile.clear()
@profile tally(a)
Profile.print(format=:flat)

 Count File                        Line Function                               
   299 ./<missing>                   -1 anonymous                              
     8 ./In[54]                       3 tally(::Array{Float64,1})              
   291 ./In[54]                       4 tally(::Array{Float64,1})              
     1 ./abstractarray.jl           485 copy!(::Array{Any,1}, ::Core.Infere... 
     1 ./float.jl                   240 +(::Float64, ::Float64)                
     1 ./inference.jl              1101 abstract_call(::Any, ::Array{Any,1}... 
     1 ./inference.jl               893 abstract_call_gf_by_type(::Any, ::A... 
     2 ./inference.jl              1152 abstract_eval(::Any, ::Array{Any,1}... 
     1 ./inference.jl              1105 abstract_eval_call(::Expr, ::Array{... 
     1 ./inference.jl              1131 abstract_eval_call(::Expr, ::Array{... 
     1 ./inference.jl              1577 typeinf_edge(::Method, ::Any, ::Sim... 
     1 ./inference.jl              1597 typeinf_edge(::Method, ::Any, ::Sim... 
     1 ./inference.jl              1603 typeinf_edge(::Method, ::Any, ::Sim... 
     1 ./inference.jl              1621 typeinf_ext(::LambdaInfo)              
     1 ./inference.jl              1786 typeinf_frame(::Core.Inference.Infe... 
     1 ./inference.jl              1677 typeinf_loop(::Core.Inference.Infer... 
     1 ./inference.jl              1457 unshare_linfo!(::LambdaInfo)           
   300 ./loading.jl                 441 include_string(::String, ::String)     
   299 ./profile.jl                  16 macro expansion;                       
   300 ./task.jl                    360 (::IJulia.##13#19)()                   
    60 ...lia/lib/julia/sys.dylib    -1 +(::Float64, ::Float64)                
     1 ...lia/lib/julia/sys.dylib    -1 abstract_call(::Any, ::Array{Any,1}... 
     1 ...lia/lib/julia/sys.dylib    -1 abstract_call_gf_by_type(::Any, ::A... 
     2 ...lia/lib/julia/sys.dylib    -1 abstract_eval(::Any, ::Array{Any,1}... 
     1 ...lia/lib/julia/sys.dylib    -1 typeinf_edge(::Method, ::Any, ::Sim... 
     1 ...lia/lib/julia/sys.dylib    -1 typeinf_edge(::Method, ::Any, ::Sim... 
     1 ...lia/lib/julia/sys.dylib    -1 typeinf_loop(::Core.Inference.Infer... 
     1 ...lia/lib/julia/sys.dylib    -1 println(::Any)                         
   300 ...IJulia/src/eventloop.jl     8 eventloop(::ZMQ.Socket)                
   300 .../src/execute_request.jl   157 execute_request(::ZMQ.Socket, ::IJu...

Memory profiling

Detailed memory profiling requires a detour. First let's write a script bar.jl, which contains the workload function tally and a wrapper for profiling.

In [58]:
;cat bar.jl

function tally(x)
    s = 0
    for v in x
        s += v
    end
    s
end

# call workload from wrapper to avoid misattribution bug
function wrapper()
    y = rand(10000)
    # force compilation
    println(tally(y))
    # clear allocation counters
    Profile.clear_malloc_data()
    # run compiled workload
    println(tally(y))
end

wrapper()

Next, in terminal, we run the script with --track-allocation=user option.

In [59]:
;julia --track-allocation=user bar.jl

4990.152520337667
4990.152520337667

The profiler outputs a file bar.jl.mem.

In [60]:
;cat bar.jl.mem

        - function tally(x)
        -     s = 0
        0     for v in x
   480000         s += v
        -     end
        0     s
        - end
        - 
        - # call workload from wrapper to avoid misattribution bug
        - function wrapper()
        -     y = rand(10000)
        -     # force compilation
        0     println(tally(y))
        -     # clear allocation counters
        0     Profile.clear_malloc_data()
        -     # run compiled workload
       96     println(tally(y))
        - end
        - 
        - wrapper()
        -

We see line 4 is allocating suspicious amount of heap memory.

Type stability

The key to writing performant Julia code is to be type stable, such that Julia is able to infer types of all variables and output of a function from the types of input arguments.

Is the tally function type stable? How to diagnose and fix it?

In [61]:
@code_warntype tally(rand(100))

Variables:
  #self#::#tally
  x::Array{Float64,1}
  s::Any
  #temp#@_4::Int64
  v::Float64
  #temp#@_6::LambdaInfo
  #temp#@_7::Float64

Body:
  begin 
      s::Any = 0 # line 3:
      #temp#@_4::Int64 = $(QuoteNode(1))
      4: 
      unless (Base.box)(Base.Bool,(Base.not_int)((#temp#@_4::Int64 === (Base.box)(Int64,(Base.add_int)((Base.arraylen)(x::Array{Float64,1})::Int64,1)))::Bool)) goto 29
      SSAValue(2) = (Base.arrayref)(x::Array{Float64,1},#temp#@_4::Int64)::Float64
      SSAValue(3) = (Base.box)(Int64,(Base.add_int)(#temp#@_4::Int64,1))
      v::Float64 = SSAValue(2)
      #temp#@_4::Int64 = SSAValue(3) # line 4:
      unless (Core.isa)(s::Union{Float64,Int64},Float64)::Any goto 14
      #temp#@_6::LambdaInfo = LambdaInfo for +(::Float64, ::Float64)
      goto 23
      14: 
      unless (Core.isa)(s::Union{Float64,Int64},Int64)::Any goto 18
      #temp#@_6::LambdaInfo = LambdaInfo for +(::Int64, ::Float64)
      goto 23
      18: 
      goto 20
      20: 
      #temp#@_7::Float64 = (s::Union{Float64,Int64} + v::Float64)::Float64
      goto 25
      23: 
      #temp#@_7::Float64 = $(Expr(:invoke, :(#temp#@_6), :(Main.+), :(s::Union{Float64,Int64}), :(v)))
      25: 
      s::Any = #temp#@_7::Float64
      27: 
      goto 4
      29:  # line 6:
      return s::Union{Float64,Int64}
  end::Union{Float64,Int64}

In this case, Julia fails to infer the type of the reduction variable s, which has to be boxed in heap memory at run time.

What's the fix?

Plotting in Julia

The three most popular options (as far as I can tell) are

  • Plots.jl (my personal favorite)
    • Defines an unified interface for plotting
    • maps arguments to different plotting "backends"
      • PyPlot, GR, PlotlyJS, and many more
In [62]:
using Plots

x = randn(50, 2);
In [63]:
pyplot()  # set the backend to PyPlot
plot(x)
Out[63]:
sys:1: MatplotlibDeprecationWarning: The set_axis_bgcolor function was deprecated in version 2.0. Use set_facecolor instead.
In [64]:
plotly()  # change backend to Plotly
plot(x)
Out[64]:
In [65]:
gr()   # change backend to GR
plot(x)
Out[65]:
10 20 30 40 50 -2 -1 0 1 2 y1 y2
In [66]:
gr()
@gif for i in 1:20
    plot(x -> sin(x) / (.2i), 0, i, xlim=(0, 20), ylim=(-.75, .75))
    scatter!(x -> cos(x) * .01 * i, 0, i, m=1)
end

INFO: Saved animation to /Users/huazhou/Documents/github.com/Hua-Zhou.github.io/teaching/biostatm280-2017spring/slides/02-juliaintro/tmp.gif
Out[66]:
In [67]:
# Nondeterministic algorithm for plotting functions
# Tries to do higher sampling where the function changes the most
scatter(sin, -3, 3)
plot!(sin)
Out[67]:
-2 0 2 -1 0 1 y1 y2
In [68]:
x = randn()
p = plot([x])
@gif for i in 1:100
    x += randn()
    push!(p, x)
end

INFO: Saved animation to /Users/huazhou/Documents/github.com/Hua-Zhou.github.io/teaching/biostatm280-2017spring/slides/02-juliaintro/tmp.gif
Out[68]:
In [ ]: