Gaussian Elimination and LU Decomposition

  • Goal: solve linear equation $$ \mathbf{A} \mathbf{x} = \mathbf{b}. $$ For simplicity we consider a square matrix $\mathbf{A} \in \mathbb{R}^{n \times n}$.

  • History: Chinese mathematical text The Nine Chapters on the Mathematical Art, Issac Newton and Carl Friedrich Gauss.

  • A toy example.

In [1]:
A = [2.0 1.0 -1.0; -3.0 -1.0 2.0; -2.0 1.0 2.0]
Out[1]:
3×3 Array{Float64,2}:
  2.0   1.0  -1.0
 -3.0  -1.0   2.0
 -2.0   1.0   2.0
In [2]:
b = [8.0; -11.0; -3.0]
Out[2]:
3-element Array{Float64,1}:
   8.0
 -11.0
  -3.0
In [3]:
# solve linear equation
A \ b
Out[3]:
3-element Array{Float64,1}:
  2.0
  3.0
 -1.0

What happens when we call A \ b to solve a linear equation?

Elementary operator matrix

  • Elementary operator matrix is the identity matrix with the 0 in position $(j,k)$ replaced by $c$ $$ \mathbf{E}_{jk}(c) = \begin{pmatrix} 1 & & \\ & \ddots & \\ & & 1 & \\ & & & \ddots & \\ & & c & & 1 & \\ & & & & & \ddots \\ & & & & & & 1 \end{pmatrix} = \mathbf{I} + c \mathbf{e}_j \mathbf{e}_k^T. $$

  • $\mathbf{E}_{jk}(c)$ is unit triangular, full rank, and its inverse is $$ \mathbf{E}_{jk}^{-1}(c) = \mathbf{E}_{jk}(-c). $$

  • $\mathbf{E}_{jk}(c)$ left-multiplies an $n \times m$ matrix $\mathbf{X}$ effectively replace its $j$-th row $\mathbf{x}_{j\cdot}$ by $c \mathbf{x}_{k \cdot} + \mathbf{x}_{j \cdot}$ $$ \mathbf{E}_{jk}(c) \times \mathbf{X} = \mathbf{E}_{jk}(c) \times \begin{pmatrix} & & \\ \cdots & \mathbf{x}_{k\cdot} & \cdots \\ & & \\ \cdots & \mathbf{x}_{j\cdot} & \cdots \\ & & \end{pmatrix} = \begin{pmatrix} & & \\ \cdots & \mathbf{x}_{k\cdot} & \cdots \\ & & \\ \cdots & c \mathbf{x}_{k\cdot} + \mathbf{x}_{j\cdot} & \cdots \\ & & \end{pmatrix}. $$ $2m$ flops.

  • Gaussian elimination applies a sequence of elementary operator matrices to transform the linear system $\mathbf{A} \mathbf{x} = \mathbf{b}$ to an upper triangular system $$ \begin{eqnarray*} \mathbf{E}_{n,n-1}(c_{n,n-1}) \cdots \mathbf{E}_{21}(c_{21}) \mathbf{A} \mathbf{x} &=& \mathbf{E}_{n,n-1}(c_{n,n-1}) \cdots \mathbf{E}_{21}(c_{21}) \mathbf{b} \\ \mathbf{U} \mathbf{x} &=& \mathbf{b}_{\text{new}}. \end{eqnarray*} $$

    Column 1:

In [4]:
E21 = [1.0 0.0 0.0; 1.5 1.0 0.0; 0.0 0.0 1.0]
Out[4]:
3×3 Array{Float64,2}:
 1.0  0.0  0.0
 1.5  1.0  0.0
 0.0  0.0  1.0
In [5]:
# zero (2, 1) entry
E21 * A
Out[5]:
3×3 Array{Float64,2}:
  2.0  1.0  -1.0
  0.0  0.5   0.5
 -2.0  1.0   2.0
In [6]:
E31 = [1.0 0.0 0.0; 0.0 1.0 0.0; 1.0 0.0 1.0]
Out[6]:
3×3 Array{Float64,2}:
 1.0  0.0  0.0
 0.0  1.0  0.0
 1.0  0.0  1.0
In [7]:
# zero (3, 1) entry
E31 * E21 * A
Out[7]:
3×3 Array{Float64,2}:
 2.0  1.0  -1.0
 0.0  0.5   0.5
 0.0  2.0   1.0
Column 2:
In [8]:
E32 = [1.0 0.0 0.0; 0.0 1.0 0.0; 0.0 -4.0 1.0]
Out[8]:
3×3 Array{Float64,2}:
 1.0   0.0  0.0
 0.0   1.0  0.0
 0.0  -4.0  1.0
In [9]:
# zero (3, 2) entry
E32 * E31 * E21 * A
Out[9]:
3×3 Array{Float64,2}:
 2.0  1.0  -1.0
 0.0  0.5   0.5
 0.0  0.0  -1.0

Gauss transformations

  • For the first column, $$ \mathbf{M}_1 = \mathbf{E}_{n1}(c_{n1}) \cdots \mathbf{E}_{31}(c_{31}) \mathbf{E}_{21}(c_{21}) = \begin{pmatrix} 1 & \\ c_{21} & \\ & \ddots & \\ c_{n1} & & 1 \end{pmatrix} $$
    For the $k$-th column, $$ \mathbf{M}_k = \mathbf{E}_{nk}(c_{nk}) \cdots \mathbf{E}_{k+1,k}(c_{k+1,k}) = \begin{pmatrix} 1 & \\ & \ddots \\ & & 1 & \\ & & c_{k+1,k} & 1\\ & & \vdots & & \ddots \\ & & c_{n,k} & & & 1 \end{pmatrix}. $$

  • $\mathbf{M}_1, \ldots, \mathbf{M}_{n-1}$ are called the Gauss transformations.

In [10]:
M1 = E31 * E21
Out[10]:
3×3 Array{Float64,2}:
 1.0  0.0  0.0
 1.5  1.0  0.0
 1.0  0.0  1.0
In [11]:
M2 = E32
Out[11]:
3×3 Array{Float64,2}:
 1.0   0.0  0.0
 0.0   1.0  0.0
 0.0  -4.0  1.0
  • Gauss transformations $\mathbf{M}_k$ are unit triangular, full rank, with inverse $$ \mathbf{M}_k^{-1} = \mathbf{E}_{k+1,k}^{-1}(c_{k+1,k}) \cdots \mathbf{E}_{nk}^{-1}(c_{nk}) = \begin{pmatrix} 1 & \\ & \ddots \\ & & 1 & \\ & & - c_{k+1,k}\\ & & \vdots & & \ddots \\ & & - c_{n,k} & & & 1 \end{pmatrix}. $$
In [12]:
inv(M1)
Out[12]:
3×3 Array{Float64,2}:
  1.0  0.0  0.0
 -1.5  1.0  0.0
 -1.0  0.0  1.0
In [13]:
inv(M2)
Out[13]:
3×3 Array{Float64,2}:
 1.0  0.0  0.0
 0.0  1.0  0.0
 0.0  4.0  1.0

LU decomposition

  • Gaussian elimination does $$ \mathbf{M}_{n-1} \cdots \mathbf{M}_1 \mathbf{A} = \mathbf{U}. $$
    Let
    $$ \mathbf{L} = \mathbf{M}1^{-1} \cdots \mathbf{M}{n-1}^{-1} = \begin{pmatrix} 1 & \

    • c_{21} & \ddots \ & & 1 & \
    • c{k+1,1}& & - c{k+1,k} & \ & & \vdots & & \ddots \
    • c{n1} & & - c{nk} & & & 1 \end{pmatrix}. $$ Thus we have the **LU decomposition** $$ \mathbf{A} = \mathbf{L} \mathbf{U}, $$ where $\mathbf{L}$ is unit lower triangular and $\mathbf{U}$ is upper triangular.

  • The whole LU algorithm is done in place, i.e., $\mathbf{A}$ is overwritten by $\mathbf{L}$ and $\mathbf{U}$.

  • LU decomposition exists if the principal sub-matrix $\mathbf{A}[1:k, 1:k]$ is non-singular for $k=1,\ldots,n-1$.

  • If the LU decomposition exists and $\mathbf{A}$ is non-singular, then the LU decmpositon is unique and $$ \det(\mathbf{A}) = \det(\mathbf{L}) \det(\mathbf{U}) = \prod_{k=1}^n u_{kk}. $$

  • The LU decomposition costs $$ 2(n-1)^2 + 2(n-2)^2 + \cdots + 2 \cdot 1^2 \approx \frac 23 n^3 \quad \text{flops}. $$

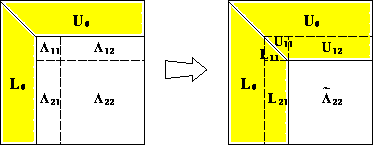
  • Actual implementations can differ: outer product LU ($kij$ loop), block outer product LU (higher level-3 fraction), Crout's algorithm ($jki$ loop).

  • Given LU decomposition $\mathbf{A} = \mathbf{L} \mathbf{U}$, solving $(\mathbf{L} \mathbf{U}) \mathbf{x} = \mathbf{b}$ for one right hand side costs $2n^2$ flops.

    • One forward substitution ($n^2$ flops) to solve $$ \mathbf{L} \mathbf{y} = \mathbf{b} $$
    • One back substitution ($n^2$ flops) to solve $$ \mathbf{U} \mathbf{x} = \mathbf{y} $$

  • Therefore to solve $\mathbf{A} \mathbf{x} = \mathbf{b}$ via LU, we need a total of $$ \frac 23 n^3 + 2n^2 \quad \text{flops}. $$

  • If there are multiple right hand sides, LU only needs to be done once.

Matrix inversion

  • For matrix inversion, there are $n$ right hand sides $\mathbf{e}_1, \ldots, \mathbf{e}_n$. Taking advantage of 0s reduces $2n^3$ flops to $\frac 43 n^3$ flops. So matrix inversion via LU costs $$ \frac 23 n^3 + \frac 43 n^3 = 2n^3 \quad \text{flops}. $$

  • No inversion mentality:

    Whenever we see matrix inverse, we should think in terms of solving linear equations.

    We do not compute matrix inverse unless

    1. it is necessary to compute standard errors
    2. number of right hand sides is much larger than $n$
    3. $n$ is small

Pivoting

  • Let $$ \mathbf{A} = \begin{pmatrix} 0 & 1 \\ 1 & 0 \\ \end{pmatrix}. $$ Is there a solution to $\mathbf{A} \mathbf{x} = \mathbf{b}$ for an arbitrary $\mathbf{b}$? Does GE/LU work for $\mathbf{A}$?

  • What if, during LU procedure, the pivot $a_{kk}$ is 0 or nearly 0 due to underflow?
    Solution: pivoting.

  • Partial pivoting: before zeroing the $k$-th column, the row with $\max_{i=k}^n |a_{ik}|$ is moved into the $k$-th row.

  • LU with partial pivoting yields $$ \mathbf{P} \mathbf{A} = \mathbf{L} \mathbf{U}, $$ where $\mathbf{P}$ is a permutation matrix, $\mathbf{L}$ is unit lower triangular with $|\ell_{ij}| \le 1$, and $\mathbf{U}$ is upper triangular.

  • Complete pivoting: Do both row and column interchanges so that the largest entry in the sub matrix A[k:n, k:n] is permuted to the $(k,k)$-th entry. This yields the decomposition $$ \mathbf{P} \mathbf{A} \mathbf{Q} = \mathbf{L} \mathbf{U}, $$ where $|\ell_{ij}| \le 1$.

  • LU decomposition with partial pivoting is the most commonly used methods for solving general linear systems. Complete pivoting is the most stable but costs more computation. Partial pivoting is stable most of times.

Implementation

  • LAPACK: ?GETRF does $\mathbf{P} \mathbf{A} = \mathbf{L} \mathbf{U}$ (LU decomposition with partial pivoting) in place.

  • R: solve() implicitly performs LU decomposition (wrapper of LAPACK routine DGESV). solve() allows specifying a single or multiple right hand sides. If none, it computes the matrix inverse. The matrix package contains lu() function that outputs L, U, and pivot.

  • Julia:

In [14]:
A
Out[14]:
3×3 Array{Float64,2}:
  2.0   1.0  -1.0
 -3.0  -1.0   2.0
 -2.0   1.0   2.0
In [15]:
# second argument indicates partial pivoting (default) or not
alu = lufact(A, Val{true})
typeof(alu)
Out[15]:
Base.LinAlg.LU{Float64,Array{Float64,2}}
In [16]:
alu[:L]
Out[16]:
3×3 Array{Float64,2}:
  1.0       0.0  0.0
  0.666667  1.0  0.0
 -0.666667  0.2  1.0
In [17]:
alu[:U]
Out[17]:
3×3 Array{Float64,2}:
 -3.0  -1.0      2.0     
  0.0   1.66667  0.666667
  0.0   0.0      0.2
In [18]:
alu[:p]
Out[18]:
3-element Array{Int64,1}:
 2
 3
 1
In [19]:
alu[:P]
Out[19]:
3×3 Array{Float64,2}:
 0.0  1.0  0.0
 0.0  0.0  1.0
 1.0  0.0  0.0
In [20]:
alu[:L] * alu[:U]
Out[20]:
3×3 Array{Float64,2}:
 -3.0  -1.0   2.0
 -2.0   1.0   2.0
  2.0   1.0  -1.0
In [21]:
A[alu[:p], :]
Out[21]:
3×3 Array{Float64,2}:
 -3.0  -1.0   2.0
 -2.0   1.0   2.0
  2.0   1.0  -1.0
In [22]:
# this is doing two triangular solves
alu \ b
Out[22]:
3-element Array{Float64,1}:
  2.0
  3.0
 -1.0
In [23]:
det(A) # this does LU!
Out[23]:
-0.9999999999999998
In [24]:
det(alu) # this is cheap
Out[24]:
-0.9999999999999998
In [25]:
inv(A) # this does LU!
Out[25]:
3×3 Array{Float64,2}:
  4.0   3.0  -1.0
 -2.0  -2.0   1.0
  5.0   4.0  -1.0
In [26]:
inv(alu) # this is cheap
Out[26]:
3×3 Array{Float64,2}:
  4.0   3.0  -1.0
 -2.0  -2.0   1.0
  5.0   4.0  -1.0

Further reading