Table of Contents¶
versioninfo()
Conjugate Gradient and Krylov Subspace Methods¶
Introduction¶
Conjugate gradient is the top-notch iterative method for solving large, structured linear systems $\mathbf{A} \mathbf{x} = \mathbf{b}$, where $\mathbf{A}$ is pd.
Earlier we talked about Jacobi, Gauss-Seidel, and successive over-relaxation (SOR) as the classical iterative solvers. They are rarely used in practice due to slow convergence.Kershaw's results for a fusion problem.
| Method | Number of Iterations |
|---|---|
| Gauss Seidel | 208,000 |
| Block SOR methods | 765 |
| Incomplete Cholesky conjugate gradient | 25 |
- History: Hestenes (UCLA professor!) and Stiefel proposed conjugate gradient method in 1950s.
Hestenes and Stiefel (1952), Methods of conjugate gradients for solving linear systems, Jounral of Research of the National Bureau of Standards.
- Solve linear equation $\mathbf{A} \mathbf{x} = \mathbf{b}$, where $\mathbf{A} \in \mathbb{R}^{n \times n}$ is pd, is equivalent to $$ \begin{eqnarray*} \text{minimize} \,\, f(\mathbf{x}) = \frac 12 \mathbf{x}^T \mathbf{A} \mathbf{x} - \mathbf{b}^T \mathbf{x}. \end{eqnarray*} $$ Denote $\nabla f(\mathbf{x}) = \mathbf{A} \mathbf{x} - \mathbf{b} =: r(\mathbf{x})$.
Conjugate gradient (CG) method¶
- Consider a simple idea: coordinate descent, that is to update components $x_j$ alternatingly. Same as the Gauss-Seidel iteration. Usually it takes too many iterations.

A set of vectors $\{\mathbf{x}^{(0)},\ldots,\mathbf{x}^{(l)}\}$ is said to be conjugate with respect to $\mathbf{A}$ if $$ \begin{eqnarray*} \mathbf{p}_i^T \mathbf{A} \mathbf{p}_j = 0, \quad \text{for all } i \ne j. \end{eqnarray*} $$ For example, eigen-vectors of $\mathbf{A}$ are conjugate to each other. Why?
Conjugate direction method: Given a set of conjugate vectors $\{\mathbf{p}^{(0)},\ldots,\mathbf{p}^{(l)}\}$, at iteration $t$, we search along the conjugate direction $\mathbf{p}^{(t)}$ $$ \begin{eqnarray*} \mathbf{x}^{(t+1)} = \mathbf{x}^{(t)} + \alpha^{(t)} \mathbf{p}^{(t)}, \end{eqnarray*} $$ where $$ \begin{eqnarray*} \alpha^{(t)} = - \frac{\mathbf{r}^{(t)T} \mathbf{p}^{(t)}}{\mathbf{p}^{(t)T} \mathbf{A} \mathbf{p}^{(t)}} \end{eqnarray*} $$ is the optimal step length.
Theorem: In conjugate direction method, $\mathbf{x}^{(t)}$ converges to the solution in at most $n$ steps.
Intuition: Look at graph.

Conjugate gradient method. Idea: generate $\mathbf{p}^{(t)}$ using only $\mathbf{p}^{(t-1)}$ $$ \begin{eqnarray*} \mathbf{p}^{(t)} = - \mathbf{r}^{(t)} + \beta^{(t)} \mathbf{p}^{(t-1)}, \end{eqnarray*} $$ where $\beta^{(t)}$ is determined by the conjugacy condition $\mathbf{p}^{(t-1)T} \mathbf{A} \mathbf{p}^{(t)} = 0$ $$ \begin{eqnarray*} \beta^{(t)} = \frac{\mathbf{r}^{(t)T} \mathbf{A} \mathbf{p}^{(t-1)}}{\mathbf{p}^{(t-1)T} \mathbf{A} \mathbf{p}^{(t-1)}}. \end{eqnarray*} $$
CG algorithm (preliminary version):
- Given $\mathbf{x}^{(0)}$
- Initialize: $\mathbf{r}^{(0)} \gets \mathbf{A} \mathbf{x}^{(0)} - \mathbf{b}$, $\mathbf{p}^{(0)} \gets - \mathbf{r}^{(0)}$, $t=0$
While $\mathbf{r}^{(0)} \ne \mathbf{0}$
- $\alpha^{(t)} \gets - \frac{\mathbf{r}^{(t)T} \mathbf{p}^{(t)}}{\mathbf{p}^{(t)T} \mathbf{A} \mathbf{p}^{(t)}}$
- $\mathbf{x}^{(t+1)} \gets \mathbf{x}^{(t)} + \alpha^{(t)} \mathbf{p}^{(t)}$
- $\mathbf{r}^{(t+1)} \gets \mathbf{A} \mathbf{x}^{(t+1)} - \mathbf{b}$
- $\beta^{(t+1)} \gets \frac{\mathbf{r}^{(t+1)T} \mathbf{A} \mathbf{p}^{(t)}}{\mathbf{p}^{(t)T} \mathbf{A} \mathbf{p}^{(t)}}$
- $\mathbf{p}^{(t+1)} \gets - \mathbf{r}^{(t+1)} + \beta^{(t+1)} \mathbf{p}^{(t)}$
- $t \gets t+1$
Remark: The initial conjugate direction $\mathbf{p}^{(0)} \gets - \mathbf{r}^{(0)}$ is crucial.
Theorem: With CG algorithm
- $\mathbf{r}^{(t)}$ are mutually orthogonal.
- $\{\mathbf{r}^{(0)},\ldots,\mathbf{r}^{(t)}\}$ is contained in the Krylov subspace of degree $t$ for $\mathbf{r}^{(0)}$, denoted by $$ \begin{eqnarray*} {\cal K}(\mathbf{r}^{(0)}; t) = \text{span} \{\mathbf{r}^{(0)},\mathbf{A} \mathbf{r}^{(0)}, \mathbf{A}^2 \mathbf{r}^{(0)}, \ldots, \mathbf{A}^{t} \mathbf{r}^{(0)}\}. \end{eqnarray*} $$
- $\{\mathbf{p}^{(0)},\ldots,\mathbf{p}^{(t)}\}$ is contained in ${\cal K}(\mathbf{r}^{(0)}; t)$.
- $\mathbf{p}^{(0)}, \ldots, \mathbf{p}^{(t)}$ are conjugate with respect to $\mathbf{A}$.
The iterates $\mathbf{x}^{(t)}$ converge to the solution in at most $n$ steps.
CG algorithm (economical version): saves one matrix-vector multiplication.
- Given $\mathbf{x}^{(0)}$
- Initialize: $\mathbf{r}^{(0)} \gets \mathbf{A} \mathbf{x}^{(0)} - \mathbf{b}$, $\mathbf{p}^{(0)} \gets - \mathbf{r}^{(0)}$, $t=0$
- While $\mathbf{r}^{(0)} \ne \mathbf{0}$
- $\alpha^{(t)} \gets \frac{\mathbf{r}^{(t)T} \mathbf{r}^{(t)}}{\mathbf{p}^{(t)T} \mathbf{A} \mathbf{p}^{(t)}}$
- $\mathbf{x}^{(t+1)} \gets \mathbf{x}^{(t)} + \alpha^{(t)} \mathbf{p}^{(t)}$
- $\mathbf{r}^{(t+1)} \gets \mathbf{r}^{(t)} + \alpha^{(t)} \mathbf{A} \mathbf{p}^{(t)}$
- $\beta^{(t+1)} \gets \frac{\mathbf{r}^{(t+1)T} \mathbf{r}^{(t+1)}}{\mathbf{r}^{(t)T} \mathbf{r}^{(t)}}$
- $\mathbf{p}^{(t+1)} \gets - \mathbf{r}^{(t+1)} + \beta^{(t+1)} \mathbf{p}^{(t)}$
- $t \gets t+1$
Computation cost per iteration is one matrix vector multiplication: $\mathbf{A} \mathbf{p}^{(t)}$.
Consider PageRank problem, $\mathbf{A}$ has dimension $n \approx 10^{10}$ but is highly structured (sparse + low rank). Each matrix vector multiplication takes $O(n)$.Theorem: If $\mathbf{A}$ has $r$ distinct eigenvalues, $\mathbf{x}^{(t)}$ converges to solution $\mathbf{x}^*$ in at most $r$ steps.
Pre-conditioned conjugate gradient (PCG)¶
Summary of conjugate gradient method for solving $\mathbf{A} \mathbf{x} = \mathbf{b}$ or equivalently minimizing $\frac 12 \mathbf{x}^T \mathbf{A} \mathbf{x} - \mathbf{b}^T \mathbf{x}$:
- Each iteration needs one matrix vector multiplication: $\mathbf{A} \mathbf{p}^{(t+1)}$. For structured $\mathbf{A}$, often $O(n)$ cost per iteration.
- Guaranteed to converge in $n$ steps.
Two important bounds for conjugate gradient algorithm:
Let $\lambda_1 \le \cdots \le \lambda_n$ be the ordered eigenvalues of a pd $\mathbf{A}$.
$$ \begin{eqnarray*} \|\mathbf{x}^{(t+1)} - \mathbf{x}^*\|_{\mathbf{A}}^2 &\le& \left( \frac{\lambda_{n-t} - \lambda_1}{\lambda_{n-t} + \lambda_1} \right)^2 \|\mathbf{x}^{(0)} - \mathbf{x}^*\|_{\mathbf{A}}^2 \\ \|\mathbf{x}^{(t+1)} - \mathbf{x}^*\|_{\mathbf{A}}^2 &\le& 2 \left( \frac{\sqrt{\kappa(\mathbf{A})}-1}{\sqrt{\kappa(\mathbf{A})}+1} \right)^{t} \|\mathbf{x}^{(0)} - \mathbf{x}^*\|_{\mathbf{A}}^2, \end{eqnarray*} $$ where $\kappa(\mathbf{A}) = \lambda_n/\lambda_1$ is the condition number of $\mathbf{A}$.
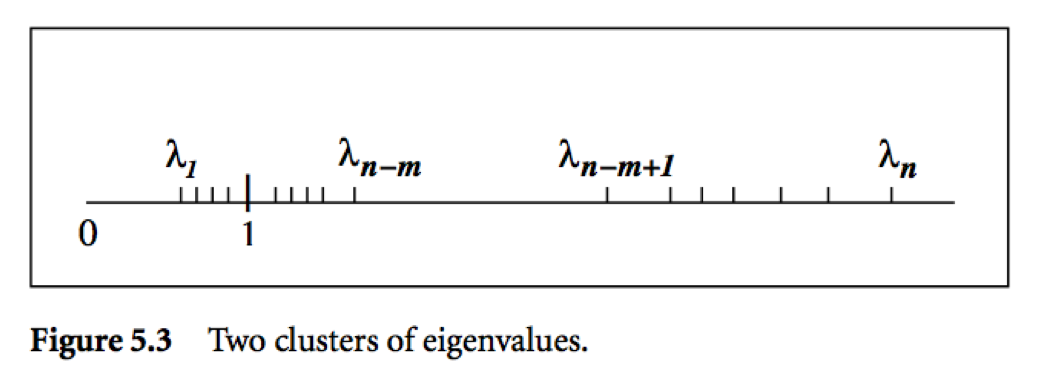

Messages:
- Roughly speaking, if the eigenvalues of $\mathbf{A}$ occur in $r$ distinct clusters, the CG iterates will approximately solve the problem after $O(r)$ steps.
- $\mathbf{A}$ with a small condition number ($\lambda_1 \approx \lambda_n$) converges fast.
Pre-conditioning: Change of variables $\widehat{\mathbf{x}} = \mathbf{C} \mathbf{x}$ via a nonsingular $\mathbf{C}$ and solve $$ (\mathbf{C}^{-T} \mathbf{A} \mathbf{C}^{-1}) \widehat{\mathbf{x}} = \mathbf{C}^{-T} \mathbf{b}. $$ Choose $\mathbf{C}$ such that
- $\mathbf{C}^{-T} \mathbf{A} \mathbf{C}^{-1}$ has small condition number, or
- $\mathbf{C}^{-T} \mathbf{A} \mathbf{C}^{-1}$ has clustered eigenvalues
- Inexpensive solution of $\mathbf{C}^T \mathbf{C} \mathbf{y} = \mathbf{r}$
Preconditioned CG does not make use of $\mathbf{C}$ explicitly, but rather the matrix $\mathbf{M} = \mathbf{C}^T \mathbf{C}$.
Preconditioned CG (PCG) algorithm:
- Given $\mathbf{x}^{(0)}$, pre-conditioner $\mathbf{M}$
- $\mathbf{r}^{(0)} \gets \mathbf{A} \mathbf{x}^{(0)} - \mathbf{b}$
- solve $\mathbf{M} \mathbf{y}^{(0)} = \mathbf{r}^{(0)}$ for $\mathbf{y}^{(0)}$
- $\mathbf{p}^{(0)} \gets - \mathbf{r}^{(0)}$, $t=0$
While $\mathbf{r}^{(0)} \ne \mathbf{0}$
- $\alpha^{(t)} \gets \frac{\mathbf{r}^{(t)T} \mathbf{y}^{(t)}}{\mathbf{p}^{(t)T} \mathbf{A} \mathbf{p}^{(t)}}$
- $\mathbf{x}^{(t+1)} \gets \mathbf{x}^{(t)} + \alpha^{(t)} \mathbf{p}^{(t)}$
- $\mathbf{r}^{(t+1)} \gets \mathbf{r}^{(t)} + \alpha^{(t)} \mathbf{A} \mathbf{p}^{(t)}$
- Solve $\mathbf{M} \mathbf{y}^{(t+1)} \gets \mathbf{r}^{(t+1)}$ for $\mathbf{y}^{(t+1)}$
- $\beta^{(t+1)} \gets \frac{\mathbf{r}^{(t+1)T} \mathbf{y}^{(t+1)}}{\mathbf{r}^{(t)T} \mathbf{r}^{(t)}}$
- $\mathbf{p}^{(t+1)} \gets - \mathbf{y}^{(t+1)} + \beta^{(t+1)} \mathbf{p}^{(t)}$
- $t \gets t+1$
Remark: Only extra cost in the pre-conditioned CG algorithm is the need to solve the linear system $\mathbf{M} \mathbf{y} = \mathbf{r}$.
Pre-conditioning is more like an art than science. Some choices include
- Incomplete Cholesky. $\mathbf{A} \approx \tilde{\mathbf{L}} \tilde{\mathbf{L}}^T$, where $\tilde{\mathbf{L}}$ is a sparse approximate Cholesky factor. Then $\tilde{\mathbf{L}}^{-1} \mathbf{A} \tilde{\mathbf{L}}^{-T} \approx \mathbf{I}$ (perfectly conditioned) and $\mathbf{M} \mathbf{y} = \tilde{\mathbf{L}} \tilde {\mathbf{L}}^T \mathbf{y} = \mathbf{r}$ is easy to solve.
- Banded pre-conditioners.
- Choose $\mathbf{M}$ as a coarsened version of $\mathbf{A}$.
- Subject knowledge. Knowledge about the structure and origin of a problem is often the key to devising efficient pre-conditioner. For example, see recent work of Stein, Chen, Anitescu (2012) for pre-conditioning large covariance matrices. http://epubs.siam.org/doi/abs/10.1137/110834469
Example of PCG¶
Preconditioners.jl wraps a bunch of preconditioners.
We use the Wathen matrix (sparse and positive definite) as a test matrix.
using BenchmarkTools, MatrixDepot, IterativeSolvers, LinearAlgebra, SparseArrays
# Wathen matrix of dimension 30401 x 30401
A = matrixdepot("wathen", 100)
using UnicodePlots
spy(A)
# sparsity level
count(!iszero, A) / length(A)
# rhs
b = ones(size(A, 1))
# solve Ax=b by CG
xcg = cg(A, b);
@benchmark cg($A, $b)
Compute the incomplete cholesky preconditioner:
using Preconditioners
@time p = CholeskyPreconditioner(A, 2)
Pre-conditioned conjugate gradient:
# solver Ax=b by PCG
xpcg = cg(A, b, Pl=p)
# same answer?
norm(xcg - xpcg)
# PCG is >10 fold faster than CG
@benchmark cg($A, $b, Pl=$p)
Other Krylov subspace methods¶
We leant about CG/PCG, which is for solving $\mathbf{A} \mathbf{x} = \mathbf{b}$, $\mathbf{A}$ pd.
MINRES (minimum residual method): symmetric indefinite $\mathbf{A}$.
Bi-CG (bi-conjugate gradient): unsymmetric $\mathbf{A}$.
Bi-CGSTAB (Bi-CG stabilized): improved version of Bi-CG.
GMRES (generalized minimum residual method): current de facto method for unsymmetric $\mathbf{A}$. E.g., PageRank problem.
Lanczos method: top eigen-pairs of a large symmetric matrix.
Arnoldi method: top eigen-pairs of a large unsymmetric matrix.
Lanczos bidiagonalization algorithm: top singular triplets of large matrix.
LSQR: least square problem $\min \|\mathbf{y} - \mathbf{X} \beta\|_2^2$. Algebraically equivalent to applying CG to the normal equation $(\mathbf{X}^T \mathbf{X} + \lambda^2 I) \beta = \mathbf{X}^T \mathbf{y}$.
LSMR: least square problem $\min \|\mathbf{y} - \mathbf{X} \beta\|_2^2$. Algebraically equivalent to applying MINRES to the normal equation $(\mathbf{X}^T \mathbf{X} + \lambda^2 I) \beta = \mathbf{X}^T \mathbf{y}$.
Software¶
Matlab¶
- Iterative methods for solving linear equations:
pcg,bicg,bicgstab,gmres, ... - Iterative methods for top eigen-pairs and singular pairs:
eigs,svds, ... Pre-conditioner:
cholinc,luinc, ...Get familiar with the reverse communication interface (RCI) for utilizing iterative solvers:
x = gmres(A, b) x = gmres(@Afun, b) eigs(A) eigs(@Afun)
Julia¶
eigsandsvdsin the Arpack.jl package. Numerical examples later.IterativeSolvers.jlpackage. CG numerical examplesLeast squares examples:
Least squares example¶
using BenchmarkTools, IterativeSolvers, LinearAlgebra, Random, SparseArrays
Random.seed!(280) # seed
n, p = 10000, 5000
X = sprandn(n, p, 0.001) # iid standard normals with sparsity 0.01
β = ones(p)
y = X * β + randn(n)
β̂_qr = X \ y
# least squares by QR
@benchmark $X \ $y
β̂_lsqr = lsqr(X, y)
@show norm(β̂_qr - β̂_lsqr)
# least squares by lsqr
@benchmark lsqr($X, $y)
β̂_lsmr = lsmr(X, y)
@show norm(β̂_qr - β̂_lsmr)
# least squares by lsmr
@benchmark lsmr($X, $y)
Use LinearMaps in iterative solvers¶
In many applications, it is advantageous to define linear maps indead of forming the actual (sparse) matrix. For a linear map, we need to specify how it acts on right- and left-multiplication on a vector. The LinearMaps.jl package is exactly for this purpose and interfaces nicely with IterativeSolvers.jl, Arnoldi.jl and other iterative solver packages.
Applications:
- The matrix is not sparse but admits special structure, e.g., easy + low rank (PageRank), Kronecker proudcts, etc.
- Less memory usage.
- Linear algebra on a standardized (centered and scaled) sparse matrix.
Consider the differencing operator that takes differences between neighboring pixels.
using LinearMaps, IterativeSolvers
# Overwrite y with A * x
# left difference assuming periodic boundary conditions
function leftdiff!(y::AbstractVector, x::AbstractVector)
N = length(x)
length(y) == N || throw(DimensionMismatch())
@inbounds for i in 1:N
y[i] = x[i] - x[mod1(i - 1, N)]
end
return y
end
# Overwrite y with A' * x
# minus right difference
function mrightdiff!(y::AbstractVector, x::AbstractVector)
N = length(x)
length(y) == N || throw(DimensionMismatch())
@inbounds for i in 1:N
y[i] = x[i] - x[mod1(i + 1, N)]
end
return y
end
# define linear map
D = LinearMap{Float64}(leftdiff!, mrightdiff!, 100; ismutating=true)
Linear maps can be used like a regular matrix.
@show size(D)
v = ones(size(D, 2)) # vector of all 1s
@show D * v
@show D' * v;
If we form the corresponding dense matrix, it will look like
Matrix(D)
If we form the corresponding sparse matrix, it will look like
using SparseArrays
sparse(D)
using UnicodePlots
spy(sparse(D))
Compute top singular values using iterative method (Arnoldi).
using Arpack
Arpack.svds(D, nsv=3)
using LinearAlgebra
# check solution against the direct method for SVD
svdvals(Matrix(D))
Compute top eigenvalues of the Gram matrix D'D using iterative method (Arnoldi).
Arpack.eigs(D'D, nev=3, which=:LM)
Further reading¶
Chapter 5 of Numerical Optimization by Jorge Nocedal and Stephen Wright (1999).
Sections 11.3-11.5 of Matrix Computations by Gene Golub and Charles Van Loan (2013).