Optimization Examples - Second Order Cone Programming (SOCP)¶
SOCP¶
A second-order cone program (SOCP) \begin{eqnarray*} &\text{minimize}& \mathbf{f}^T \mathbf{x} \\ &\text{subject to}& \|\mathbf{A}_i \mathbf{x} + \mathbf{b}_i\|_2 \le \mathbf{c}_i^T \mathbf{x} + d_i, \quad i = 1,\ldots,m \\ & & \mathbf{F} \mathbf{x} = \mathbf{g} \end{eqnarray*} over $\mathbf{x} \in \mathbb{R}^n$. This says the points $(\mathbf{A}_i \mathbf{x} + \mathbf{b}_i, \mathbf{c}_i^T \mathbf{x} + d_i)$ live in the second order cone (ice cream cone, Lorentz cone, quadratic cone) \begin{eqnarray*} \mathbf{Q}^{n+1} = \{(\mathbf{x}, t): \|\mathbf{x}\|_2 \le t\} \end{eqnarray*} in $\mathbb{R}^{n+1}$.
QP is a special case of SOCP. Why?
When $\mathbf{c}_i = \mathbf{0}$ for $i=1,\ldots,m$, SOCP is equivalent to a quadratically constrained quadratic program (QCQP) \begin{eqnarray*} &\text{minimize}& (1/2) \mathbf{x}^T \mathbf{P}_0 \mathbf{x} + \mathbf{q}_0^T \mathbf{x} \\ &\text{subject to}& (1/2) \mathbf{x}^T \mathbf{P}_i \mathbf{x} + \mathbf{q}_i^T \mathbf{x} + r_i \le 0, \quad i = 1,\ldots,m \\ & & \mathbf{A} \mathbf{x} = \mathbf{b}, \end{eqnarray*} where $\mathbf{P}_i \in \mathbf{S}_+^n$, $i=0,1,\ldots,m$. Why?
A rotated quadratic cone in $\mathbb{R}^{n+2}$ is \begin{eqnarray*} \mathbf{Q}_r^{n+2} = \{(\mathbf{x}, t_1, t_2): \|\mathbf{x}\|_2^2 \le 2 t_1 t_2, t_1 \ge 0, t_2 \ge 0\}. \end{eqnarray*} A point $\mathbf{x} \in \mathbb{R}^{n+1}$ belongs to the second order cone $\mathbf{Q}^{n+1}$ if and only if \begin{eqnarray*} \begin{pmatrix} \mathbf{I}_{n-2} & 0 & 0 \\ 0 & - 1/\sqrt 2 & 1 / \sqrt 2 \\ 0 & 1/\sqrt 2 & 1 / \sqrt 2 \end{pmatrix} \mathbf{x} \end{eqnarray*} belongs to the rotated quadratic cone $\mathbf{Q}_r^{n+1}$.
Gurobi allows users to input second order cone constraint and quadratic constraints directly.
Mosek allows users to input second order cone constraint, quadratic constraints, and rotated quadratic cone constraint directly.
Following sets are (rotated) quadratic cone representable sets:
(Absolute values) $|x| \le t \Leftrightarrow (x, t) \in \mathbf{Q}^2$.
Euclidean norms) $\|\mathbf{x}\|_2 \le t \Leftrightarrow (\mathbf{x}, t) \in \mathbf{Q}^{n+1}$.
(Sume of squares) $\|\mathbf{x}\|_2^2 \le t \Leftrightarrow (\mathbf{x}, t, 1/2) \in \mathbf{Q}_r^{n+2}$.
(Ellipsoid) For $\mathbf{P} \in \mathbf{S}_+^n$ and if $\mathbf{P} = \mathbf{F}^T \mathbf{F}$, where $\mathbf{F} \in \mathbf{R}^{n \times k}$, then \begin{eqnarray*} & & (1/2) \mathbf{x}^T \mathbf{P} \mathbf{x} + \mathbf{c}^T \mathbf{x} + r \le 0 \\ &\Leftrightarrow& \mathbf{x}^T \mathbf{P} \mathbf{x} \le 2t, t + \mathbf{c}^T \mathbf{x} + r = 0 \\ &\Leftrightarrow& (\mathbf{F} \mathbf{x}, t, 1) \in \mathbf{Q}_r^{k+2}, t + \mathbf{c}^T \mathbf{x} + r = 0. \end{eqnarray*} Similarly, \begin{eqnarray*} \|\mathbf{F} (\mathbf{x} - \mathbf{c})\|_2 \le t \Leftrightarrow (\mathbf{y}, t) \in \mathbf{Q}^{n+1}, \mathbf{y} = \mathbf{F}(\mathbf{x} - \mathbf{c}). \end{eqnarray*} This fact shows that QP and QCQP are instances of SOCP.
(Second order cones) $\|\mathbf{A} \mathbf{x} + \mathbf{b}\|_2 \le \mathbf{c}^T \mathbf{x} + d \Leftrightarrow (\mathbf{A} \mathbf{x} + \mathbf{b}, \mathbf{c}^T \mathbf{x} + d) \in \mathbf{Q}^{m+1}$.
(Simple polynomial sets) \begin{eqnarray*} \{(t, x): |t| \le \sqrt x, x \ge 0\} &=& \{ (t,x): (t, x, 1/2) \in \mathbf{Q}_r^3\} \\ \{(t, x): t \ge x^{-1}, x \ge 0\} &=& \{ (t,x): (\sqrt 2, x, t) \in \mathbf{Q}_r^3\} \\ \{(t, x): t \ge x^{3/2}, x \ge 0\} &=& \{ (t,x): (x, s, t), (s, x, 1/8) \in \mathbf{Q}_r^3\} \\ \{(t, x): t \ge x^{5/3}, x \ge 0\} &=& \{ (t,x): (x, s, t), (s, 1/8, z), (z, s, x) \in \mathbf{Q}_r^3\} \\ \{(t, x): t \ge x^{(2k-1)/k}, x \ge 0\}&,& k \ge 2, \text{can be represented similarly} \\ \{(t, x): t \ge x^{-2}, x \ge 0\} &=& \{ (t,x): (s, t, 1/2), (\sqrt 2, x, s) \in \mathbf{Q}_r^3\} \\ \{(t, x, y): t \ge |x|^3/y^2, y \ge 0\} &=& \{ (t,x,y): (x, z) \in \mathbf{Q}^2, (z, y/ 2, s), (s, t/2, z) \in \mathbf{Q}_r^3\} \end{eqnarray*}
(Geometric mean) The hypograph of the (concave) geometric mean function \begin{eqnarray*} \mathbf{K}_{\text{gm}}^n = \{(\mathbf{x}, t) \in \mathbb{R}^{n+1}: (x_1 x_2 \cdots x_n)^{1/n} \ge t, \mathbf{x} \succeq \mathbf{0}\} \end{eqnarray*} can be represented by rotated quadratic cones. For example, \begin{eqnarray*} \mathbf{K}_{\text{gm}}^2 &=& \{(x_1, x_2, t): \sqrt{x_1 x_2} \ge t, x_1, x_2 \ge 0\} \\ &=& \{(x_1, x_2, t): (\sqrt 2 t, x_1, x_2) \in \mathbf{Q}_r^3\}. \end{eqnarray*}
(Harmonic mean) The hypograph of the harmonic mean function $\left( n^{-1} \sum_{i=1}^n x_i^{-1} \right)^{-1}$ can be represented by rotated quadratic cones \begin{eqnarray*} & & \left( n^{-1} \sum_{i=1}^n x_i^{-1} \right)^{-1} \ge t, \mathbf{x} \succeq \mathbf{0} \\ &\Leftrightarrow& n^{-1} \sum_{i=1}^n x_i^{-1} \le y, \mathbf{x} \succeq \mathbf{0} \\ &\Leftrightarrow& x_i z_i \ge 1, \sum_{i=1}^n z_i = ny, \mathbf{x} \succeq \mathbf{0} \\ &\Leftrightarrow& 2 x_i z_i \ge 2, \sum_{i=1}^n z_i = ny, \mathbf{x} \succeq \mathbf{0}, \mathbf{z} \succeq \mathbf{0} \\ &\Leftrightarrow& (\sqrt 2, x_i, z_i) \in \mathbf{Q}_r^3, \mathbf{0}^T \mathbf{z} = ny, \mathbf{x} \succeq \mathbf{0}, \mathbf{z} \succeq \mathbf{0}. \end{eqnarray*}
(Convex increasing rational powers) For $p,q \in \mathbf{Z}_+$ and $p/q \ge 1$, \begin{eqnarray*} \mathbf{K}^{p/q} = \{(x, t): x^{p/q} \le t, x \ge 0\} = \{(x,t): (t\mathbf{1}_q, \mathbf{1}_{p-q}, x) \in \mathbf{K}_{\text{gm}}^p\}. \end{eqnarray*}
(Convex decreasing rational powers) For any $p,q \in \mathbf{Z}_+$, \begin{eqnarray*} \mathbf{K}^{-p/q} = \{(x, t): x^{-p/q} \le t, x \ge 0\} = \{(x,t): (x\mathbf{1}_p, t\mathbf{1}_{q}, 1) \in \mathbf{K}_{\text{gm}}^{p+q}\}. \end{eqnarray*}
(Power cones) The power cone with rational powers is \begin{eqnarray*} \mathbf{K}_{\alpha}^{n+1} = \left\{ (\mathbf{x},y) \in \mathbb{R}_+^n \times \mathbb{R}: |y| \le \prod_{j=1}^n x_j^{p_j/q_j} \right\}, \end{eqnarray*} where $p_j, q_j$ are integers satisfying $0 < p_j \le q_j$ and $\sum_{j=1}^n p_j/q_j = 1$. Let $\beta = \text{lcm}(q_1,\ldots, q_n)$ and \begin{eqnarray*} s_j = \beta \sum_{k=1}^j \frac{p_k}{q_k}, \quad j=1,\ldots,n-1. \end{eqnarray*} Then it can be represented as \begin{eqnarray*} & & |y| \le (z_1 z_2 \cdots z_\beta)^{1/q} \\ & & z_1 = \cdots = z_{s_1} = x_1, \quad z_{s_1+1} = \cdots = z_{s_2} = x_2, \quad z_{s_{n-1}+1} = \cdots = z_\beta = x_n. \end{eqnarray*}
References for above examples: Papers Lobo, Vandergerghe, Boyd, Lebret (1998)10032-0), Alizadeh and Goldfarb (2003), and book by Ben-Tal and Nemirovski (2001). Now our catalogue of SOCP terms includes all above terms.
Most of these function are implemented as the built-in function in the convex optimization modeling language cvx (for Matlab) or Convex.jl (for Julia).
SOCP example: group lasso¶
In many applications, we need to perform variable selection at group level. For instance, in factorial analysis, we want to select or de-select the group of regression coefficients for a factor simultaneously. Yuan and Lin (2006) propose the group lasso that \begin{eqnarray*} &\text{minimize}& \frac 12 \|\mathbf{y} - \beta_0 \mathbf{1} - \mathbf{X} \beta\|_2^2 + \lambda \sum_{g=1}^G w_g \|\beta_g\|_2, \end{eqnarray*} where $\beta_g$ is the subvector of regression coefficients for group $g$, and $w_g$ are fixed group weights. This is equivalent to the SOCP \begin{eqnarray*} &\text{minimize}& \frac 12 \beta^T \mathbf{X}^T \left(\mathbf{I} - \frac{\mathbf{1} \mathbf{1}^T}{n} \right) \mathbf{X} \beta + \\ & & \quad \mathbf{y}^T \left(\mathbf{I} - \frac{\mathbf{1} \mathbf{1}^T}{n} \right) \mathbf{X} \beta + \lambda \sum_{g=1}^G w_g t_g \\ &\text{subject to}& \|\beta_g\|_2 \le t_g, \quad g = 1,\ldots, G, \end{eqnarray*} in variables $\beta$ and $t_1,\ldots,t_G$.
Overlapping groups are allowed here.
SOCP example: sparse group lasso¶
- \begin{eqnarray*} &\text{minimize}& \frac 12 \|\mathbf{y} - \beta_0 \mathbf{1} - \mathbf{X} \beta\|_2^2 + \lambda_1 \|\beta\|_1 + \lambda_2 \sum_{g=1}^G w_g \|\beta_g\|_2 \end{eqnarray*} achieves sparsity at both group and individual coefficient level and can be solved by SOCP as well.
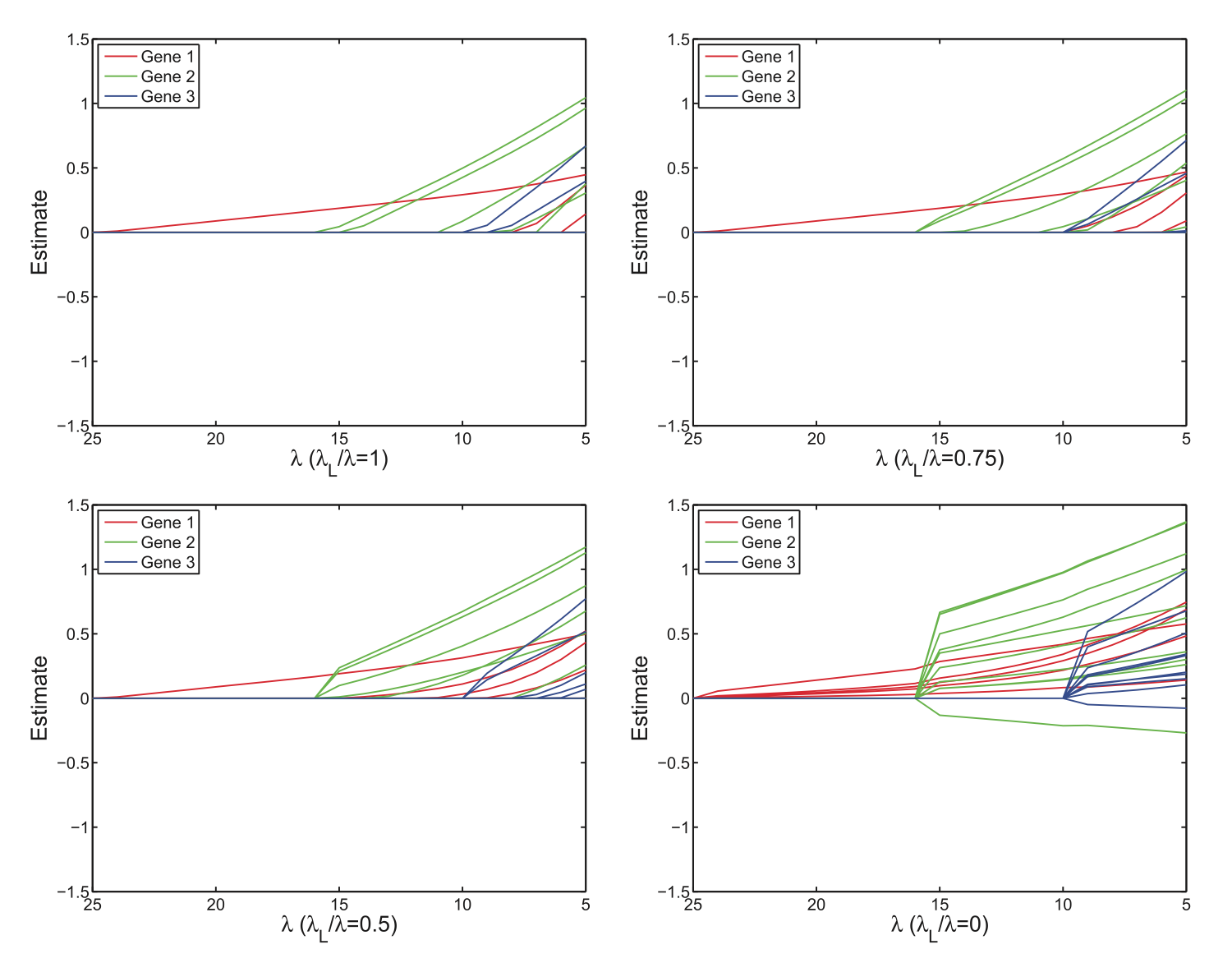
- Apparently we can solve any previous loss functions (quantile, $\ell_1$, composite quantile, Huber, multi-response model) plus group or sparse group penalty by SOCP.
SOCP example: square-root lasso¶
Belloni, Chernozhukov, and Wang (2011) minimizes \begin{eqnarray*} \|\mathbf{y} - \beta_0 \mathbf{1} - \mathbf{X} \beta\|_2 + \lambda \|\beta\|_1 \end{eqnarray*} by SOCP. This variant generates the same solution path as lasso (why?) but simplifies the choice of $\lambda$.
A demo example: http://hua-zhou.github.io/teaching/biostatm280-2016winter/lasso.html
SOCP example: image denoising by ROF model¶
SOCP example: $\ell_p$¶
- $\ell_p$ regression with $p \ge 1$ a rational number \begin{eqnarray*} &\text{minimize}& \|\mathbf{y} - \mathbf{X} \beta\|_p \end{eqnarray*} can be formulated as a SOCP. Why? For instance, $\ell_{3/2}$ regression combines advantage of both robust $\ell_1$ regression and least squares.