Disciplined Convex Programming¶
Convex optimization problems¶
A mathematical optimization problem, or just optimization problem, has the form $$ \begin{eqnarray*} &\text{minimize}& f_0(\mathbf{x}) \\ &\text{subject to}& f_i(\mathbf{x}) \le b_i, \quad i = 1,\ldots,m. \end{eqnarray*} $$ Here $f_0: \mathbb{R}^n \mapsto \mathbb{R}$ is the objective function and $f_i:\mathbb{R}^n \mapsto \mathbb{R}$, $i=1,\ldots,m$, are the constraint functions.
An equality constraint $f_i(\mathbf{x}) = b_i$ can be absorbed into inequality constraints $f_i(\mathbf{x}) \le b_i$ and $- f_i(\mathbf{x}) \le - b_i$.
If the objective and constraint functions are convex, then it is called a convex optimization problem.
In a convex optimization problem, only linear equality constraint of form $\mathbf{A} \mathbf{x} = \mathbf{b}$ is allowed (why?).Convex programming (LS, LP, QP, GP, SOCP, SDP) is becoming a technology (
Mosek,Gurobi,Cplex,cvx,Convex.jl, ...), just like numerical linear algebra libraries BLAS and LAPACK. Current technology can solve convex problems with up to thousands of variables and constraints.
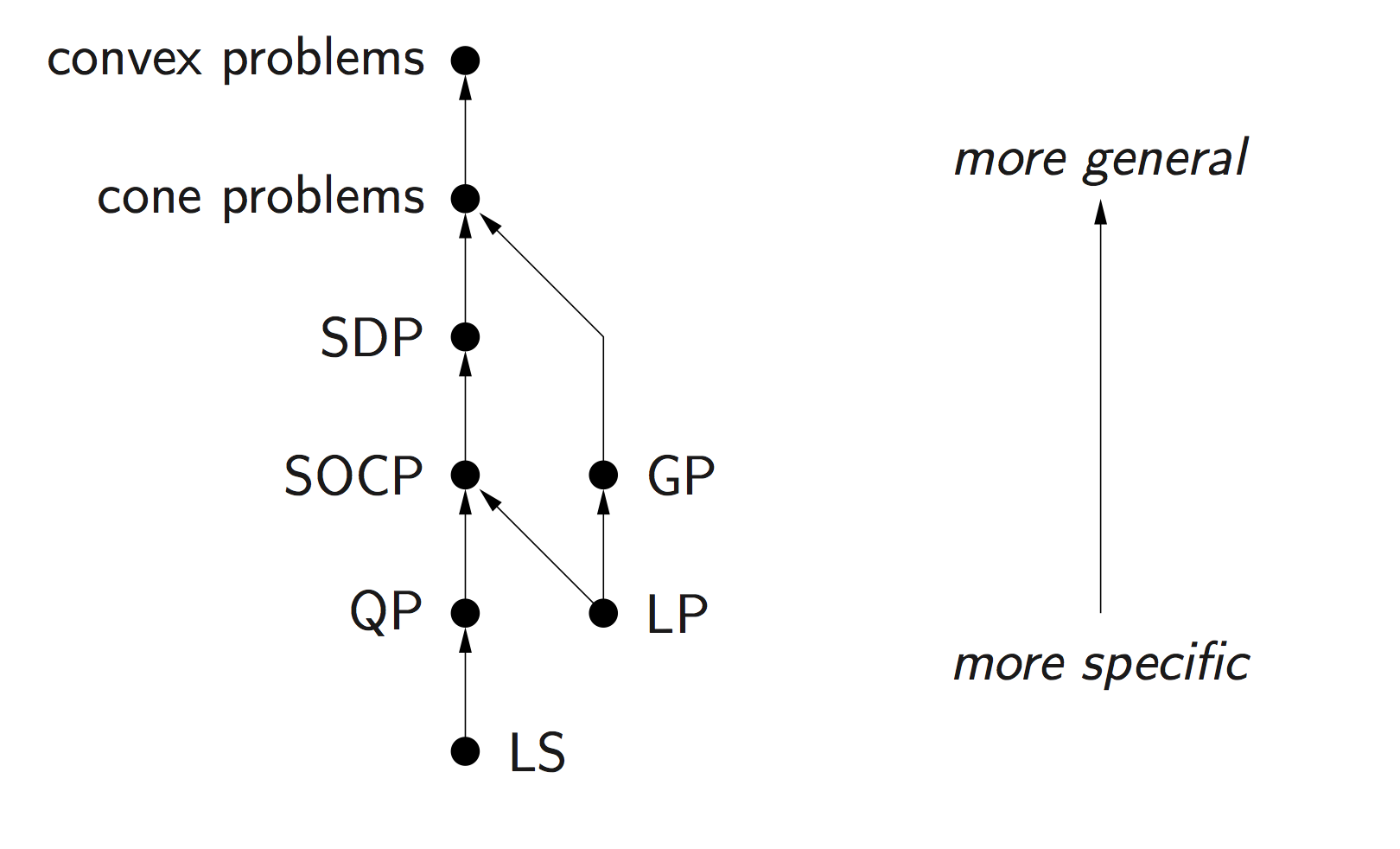
A definite resource is the book Convex Optimization by Boyd and Vandenberghe, which is freely available at http://stanford.edu/~boyd/cvxbook/. Same website has links to slides, code, and lecture videos.

Lecture videos:
http://www.stanford.edu/class/ee364a/videos.html
http://www.stanford.edu/class/ee364b/videos.htmlUCLA courses by Lieven Vandenberghe: EE236A (Linear Programming), EE236B (Convex Optimization), EE236C (Optimization Methods for Large-scale Systems).
Optimization software¶
Like numerical linear algebra, getting familiar with good optimization softwares broadens the scope and scale of problems we are able to solve in statistics.
Following table lists some of the best convex optimization softwares. Use of modeling tools
cvx(for Matlab) orConvex.jl(for Julia), coupled with solversMosekand/orGurobi, is highly recommended.
| LP | MILP | SOCP | MISOCP | SDP | GP | NLP | MINLP | R | Matlab | Julia | Python | Cost | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| modeling tools | ||||||||||||||||
| MathProgBase.jl | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | O | ||||||||
| Convex.jl | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | O | |||||||||
| cvx | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | A | |||||||
| convex solvers | ||||||||||||||||
| Mosek | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | A | ||||
| Gurobi | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | A | |||||||
| CPLEX | ✔️ | ✔️ | ✔️ | ✔️ | ? | ✔️ | ✔️ | ✔️ | A | |||||||
| SCS | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | O | |||||||||
| SeDuMi | ✔️ | ✔️ | ✔️ | ? | ✔️ | O | ||||||||||
| SDPT3 | ✔️ | ✔️ | ✔️ | ? | ✔️ | O | ||||||||||
| NLP solvers | ||||||||||||||||
| KNITRO | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | $ | |||||||
| NLopt | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | O | ||||||||||
| Ipopt | ✔️ | ✔️ | ✔️ | ✔️ | ✔️ | O |
- O: open source
- A: free academic license
$: commercial
Difference between modeling tool and solvers.
Solvers (
Mosek,Gurobi,Cplex, ...) are concrete software implementation of optimization algorithms.Modeling tools such as
cvx(for Matlab) andConvex.jl(Julia analog of cvx) implement the disciplined convex programming (DCP) paradigm proposed by Grant and Boyd (2008) http://stanford.edu/~boyd/papers/disc_cvx_prog.html. DCP prescribes a set of simple rules from which users can construct convex optimization problems easily.Modeling tools usually have the capability to use a variety of solvers. But modeling tools are solver agnostic so users do not have to worry about specific solver interface.
LP examples¶
Compressive sensing (Candes, Tao, Donoho).
http://hua-zhou.github.io/teaching/biostatm280-2016winter/cs.html$L_1$, $L_\infty$ regression, Quantile regression, Dantzig selector (Candes, Tao), 1-norm svm.
http://hua-zhou.github.io/teaching/st790-2015spr/ST790-2015-HW4.pdf
QP and SOCP examples¶
Nonnegative least squares (NNLS), Lasso regression, Elastic net, generalized lasso, support vector machine (svm), Huber loss regression.
Group lasso, square root lasso, image denoising.
http://hua-zhou.github.io/teaching/biostatm280-2016winter/lasso.html
http://hua-zhou.github.io/teaching/st790-2015spr/ST790-2015-HW5.pdf
SDP¶
- Expriment design, matrix completion.
http://hua-zhou.github.io/teaching/st790-2015spr/ST790-2015-HW6.pdf
GP¶
- Logistic regression, Bradley-Terry.